定義
 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率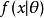 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率假設我們需要根據觀察數據 估計沒有觀察到的總體參數 ,讓 作為 的採樣分布,這樣 就是總體參數為 時的機率。函式
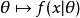 最大後驗機率
最大後驗機率即為似然函式,其估計
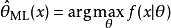 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率就是的最大似然估計。
 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率假設存在一個先驗分布,這就允許我們將作為貝葉斯統計(en:Bayesian statistics)中的隨機變數,這樣的後驗分布就是:
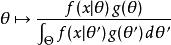 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率其中是的domain,這是貝葉斯定理的直接套用。
 最大後驗機率
最大後驗機率最大後驗估計方法於是估計為這個隨機變數的後驗分布的眾數:
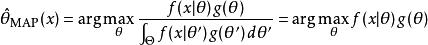 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率 最大後驗機率
最大後驗機率後驗分布的分母與無關,所以在最佳化過程中不起作用。注意當前驗是常數函式時最大後驗估計與最大似然估計重合。
方法
最大後驗估計可以用以下幾種方法計算:
解析方法,當後驗分布的模能夠用解析解方式表示的時候用這種方法。當使用共軛先驗的時候就是這種情況。
通過如共扼積分法或者牛頓法這樣的數值最佳化方法進行,這通常需要一階或者導數,導數需要通過解析或者數值方法得到。
通過期望最大化算法的修改實現,這種方法不需要後驗密度的導數。
1.解析方法,當後驗分布的模能夠用解析解方式表示的時候用這種方法。當使用共軛先驗的時候就是這種情況。
2.通過如共扼積分法或者牛頓法這樣的數值最佳化方法進行,這通常需要一階或者導數,導數需要通過解析或者數值方法得到。
3.通過期望最大化算法的修改實現,這種方法不需要後驗密度的導數。
儘管最大後驗估計與 Bayesian 統計共享前驗分布的使用,通常並不認為它是一種 Bayesian 方法,這是因為最大後驗估計是點估計,然而 Bayesian 方法的特點是使用這些分布來總結數據、得到推論。Bayesian 方法試圖算出後驗均值或者中值以及posterior interval,而不是後驗模。尤其是當後驗分布沒有一個簡單的解析形式的時候更是這樣:在這種情況下,後驗分布可以使用Markov chain Monte Carlo技術來模擬,但是找到它的模的最佳化是很困難或者是不可能的。
計算
MAP估計可以通過以下幾種方式計算:
1、分析地,當後分布的模式可以以封閉形式給出時。 當使用共軛前體時就是這種情況。
2、通過數值最佳化,如共軛梯度法或牛頓法。 這通常需要一階或二階導數,必須通過分析或數值方法進行評估。
3、通過修改期望最大化算法。 這不需要後密度的導數。
4、通過使用模擬退火的蒙特卡羅方法。
評價
雖然MAP估計只需要溫和的條件就是貝葉斯估計的一個極限情況(在0-1損失函式下),但它一般不能很好地代表貝葉斯方法。 這是因為MAP估計是點估計,而貝葉斯方法的特徵在於使用分布來總結數據和繪製推論:因此,貝葉斯方法傾向於報告後驗均值或中值,以及可信區間。 這是因為這些估計量分別在平方誤差和線性誤差損失下是最優的 - 這更能代表典型的損失函式 - 並且因為後驗分布可能沒有簡單的分析形式:在這種情況下,可以模擬分布 使用馬爾可夫鏈蒙特卡羅技術,而最佳化以找到其模式可能是困難的或不可能的。
在許多類型的模型中,例如混合模型,後部可以是多模態的。在這種情況下,通常的建議是應該選擇最高模式:這並不總是可行的(全局最佳化是一個難題),在某些情況下甚至不可能(例如在出現可識別性問題時)。此外,最高模式可能是大多數後驗的不典型。
最後,與ML估計器不同,MAP估計在重新參數化下不是不變的。從一個參數化切換到另一個參數化涉及引入影響最大值位置的雅可比行列式 。
作為上述貝葉斯估計量(均值和中位數估計量)與使用MAP估計值之間差異的一個例子,考慮需要將輸入x分類為正或負的情況(例如,貸款有風險或安全) 。假設關於正確的分類方法h1,h2和h3隻有三種可能的假設,後驗分別為0.4,0.3和0.3。假設給定一個新實例,x,h1將其分類為正數,而另外兩個將其分類為負數。使用對正確分類器h1的MAP估計,x被分類為正,而貝葉斯估計器將對所有假設求平均並將x分類為負。
