定義及內容
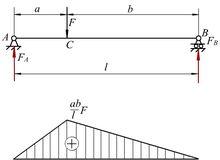彎矩 圖3彎矩是受力構件截面上的內力矩的一種，即垂直於橫截面的內力系的合力偶矩。其大小為該截面截取的構件部分上所有外力對該截面形心矩的代數和，其正負約定為是構件下凹為正，上凸為負(正負區分標準是構件上部受壓為正，下部受壓為負；反之構件上部受拉為負，下部受拉為正。在土木工程中，彎矩圖習慣繪於桿件受拉一側，在圖上可不註明正負號)。比如說一個懸臂樑，當梁端力為2kN，梁長為3m，剛固端彎矩為-6kN·m，而梁的跨中彎矩為-3kN·m，按這個做法可以簡單算，不過更深的算法要見《材料力學》了 。
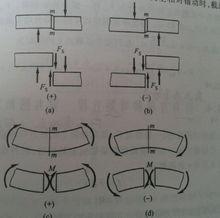
圖4中，M就是彎矩作用，v就是剪力作用，n就是軸力作用。
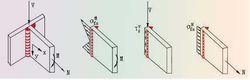彎矩 圖4區分正負
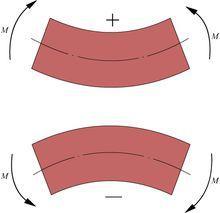彎矩 圖1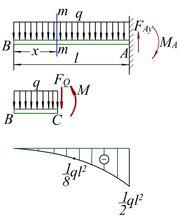
彎矩 圖2一般而言，在不同的學科中彎矩的正負有不同的規定。規定了彎矩的正負，就可以將彎矩進行代數計算。
在列彎矩計算時，套用“左上右下為正，左下右上為負”的判別方法。凡截面左側樑上外力對截面形心之矩為順時針轉向，或截面右側外力對截面形心之矩為逆時針轉向，都將產生正的彎矩，故均取正號；反之為負，即 左順右逆，彎矩為正 。
對於土木工程結構中的一根梁（指水平向的構件），當構件區段下側受拉時，我們稱此區段所受彎矩為正彎矩；當構件區段上側受拉時，我們稱此區段所受彎矩為負彎矩。
PKPM給出的彎矩方向：
作用力方向（對基礎）：軸力 N 壓為正（↓）；
彎矩 M 順時針為正（-↓）；
剪力 V 順時針為正（→）。
計算公式
彎矩公式：
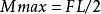彎矩(M表示最大彎矩，F表示外力，L即為力臂)。
彎矩圖
彎矩圖彎矩圖是一種圖線，用來表示梁的各橫截面上彎矩沿軸線的變化情況。總結規律如下：
（1）在梁的某一段內，若無分布載荷作用，即q(x)=0，由d²M(x)/dx²=q(x)=0可知，M(x)是x的一次函式，彎矩圖是斜直線。
（2）在梁的某一段內，若作用分布載荷作用，即q(x)=常數，則d²M(x)/dx²=q(x)=常數，可以得到M(x)是x的二次函式。彎矩圖是拋物線。
（3）在梁的某一截面內，若F(x)=dM(x)/dx=0,則在這一截面上彎矩有一極值（極大或極小）。即彎矩的極值發生在剪力為零的截面上。
疊加原理
圖6-9 a、b、c分別畫出了同一根粱AB受q、M兩種載荷作用、q單獨作用及M單獨作用的三種受力情況。
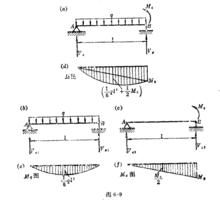疊加原理圖在q、M共同作用時
V=ql/2+M/l V=ql/2+M/l
原理推導從計算結果中可以看到，梁的支座反力和彎矩都是荷載(q、M)的一次函式，即反力或彎矩與荷載成線性關係。這時，g、M共同作用F所產生的反力或彎矩等於g與M單獨作用時所產生的反力或彎矩的代數和：
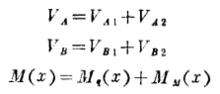推導過程這種關係不僅在本例中存在，而且在其他力學計算中普遍存在， 即只要反力、彎矩（或其他量）與載荷成線性關係，則若干個載荷共同引起的反力、彎矩（或其他量）等於各個載荷單獨引起的反力、彎矩（或其他量）相疊加。這種關係稱為疊加原理。套用疊加原理的前提是構件處在小變形情況下，這時各荷載對構件的影響各自獨立。
