定義
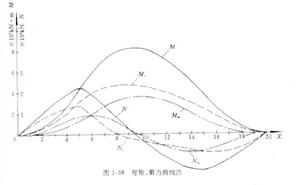
波浪彎矩曲線指船體梁的波浪附加彎矩的曲線。
波浪附加彎矩完全是由波浪產生的附加浮力（相對於靜水狀態的浮力增量）引起的，簡稱波浪彎矩。
波浪產生的附加浮力是隨機的、動態的，其計算十分複雜。
傳統的方法，都是將船舶靜置於標準波浪上求取波浪附加浮力的，即假想船舶以波速在波浪的傳播方向上航行，此時船與波的相對速度為零。這樣，求得的波浪附加浮力是靜態的，其對應的波浪附加彎矩稱為靜波浪彎矩。
當所有船舶都在同一計算原理的基礎上進行比較時．該方法在一定範圍內仍然是適用的，即對動波浪彎矩仍可在形式上保留靜置計算法。
綜上所述，通常按如下步驟計算船體梁所受到的彎矩：
①計算重量分布曲線p(x)；
②計算靜水浮力曲線b(x)；
③計算靜水載荷曲線q(x)：
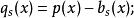波浪彎矩曲線④計算靜水彎矩：
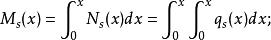波浪彎矩曲線⑤計算靜波浪彎矩：
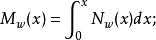波浪彎矩曲線⑥計算總縱彎矩：
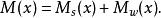波浪彎矩曲線其中，N(x)和N(x)分別指靜水剪力和靜波浪剪力。
計算
船舶由靜水進入波浪時，重量曲線p(x)並未改變，但水線面發生了變化，從而導致浮力的重新分布。波浪下浮力曲線相對靜水狀態的浮力增量是引起靜波浪彎矩的載荷。由此可知，靜波浪彎矩與船型、波浪要素以及船舶與波浪的相對位置有關。
傳統算法歸納如下：
①將船舶靜置於波浪上，即假想船舶以波速在波浪的傳播方向上航行，船舶與波浪處於相對靜止狀態；
②以二維坦谷波作為標準波形，計算波長等於船長（內河船舶斜置於一個波長上），計算波高按有關規範或強度標準選取；
③取波峰位於船中及波谷位於船中兩種狀態分別進行計算。
由於在確定計算波高時帶有很大的主觀性，故傳統的船舶總縱強度計算帶有假定性，因此計算過分精確也是沒有意義的。
坦谷波的繪製
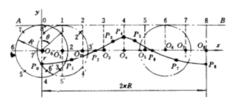圖1 坦谷波的繪製若以半徑為R的圓盤（稱為滾圓），沿直線AB滾動時，圓內一距圓心為r的定點P所描繪的軌跡，即為一坦谷波曲線。坦谷波曲線可按圖1所示的方法繪製。將直線AB（即波長λ）及滾圓圓周各分為數量相同的n等分（通常為八等分），分別以各等分點為中心，順次將滾圓逆時針旋轉360°/n，記下P點的不同位置，連線各點的光滑曲線便為一坦谷波曲線。
