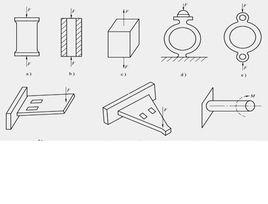
基本概念
彈性物體因外力產生形變後的恢復力 。 簡稱彈力。形變也存在於物體內部,因此物體內部的各部分間都有彈性力相作用。彈性力有各種名稱:相互壓縮時,稱壓力,垂直於物體表面的壓力稱法向壓力;相互拉長時,稱張力。物體給平面或斜面的法向壓力的反作用力,稱支持力或反力,實質上也是壓力。一定範圍內彈性力和變形程度成正比,這個範圍稱彈性限度。在限度內,撤去外力,物體能恢復原狀;超過這限度,變形程度不再和外力成正比,撤去外力後物體也不能恢復原狀。對彈簧來說,彈性力為 F=- kx, x表示彈簧終端的位移, k為彈性力和位移值之比,稱剛度係數,負號表示彈性力的方向與位移的方向相反。彈性力也是保守力,彈性力作功可用彈性勢能表示 ,其值為 , x為位移的值。
在外力作用下彈性物體形變後所產生的一種恢復力。 彈性力的特點是它在變形體上所做的功並不轉化為熱, 但可轉化為勢能。彈性力是一種保守力。物體中任何兩個質點相對位置的變化,稱為物體變形。當物體的形變很小時,彈性力F和物體中質點M開平衡位置時的位移成正比,其方向指向力圖使質點復到平衡位置的方向。包括風化作用、侵蝕作用、搬運作用、沉積作用和固結成岩作用。指由太陽輻射、重力、日月引力、水流、風力等來自地球外部的營力(通過大氣、水、生物等)所引起的作用。來自地球外部,主要是太陽輻射能,包括風化、堆積、侵蝕、搬運固結成岩作用等。
相關知識
彈性力學比較偏重數學,尋求一些特殊問題的解析解答,常採用偏微分方程中的求解方法,對高數要求較高。我們上的彈性力學主要討論彈性力學數學方法,就是套用數學分析工具建立彈性力學的基本方程和基礎理論,並且根據邊界條件求解彈性體的應力場和位移場。彈性力學的基本方程,在數學上,是偏微分方程的邊值問題,求解的方法有解析法和近似解法。解析法,即直接求解偏微分方程邊值問題,這在數學上難度極大,因此僅適用於個別特殊邊界條件問題。由於解析方法的套用困難,因此近似解法在彈性力學的發展中有著重要意義。
 彈性力
彈性力彈性力學,是固體力學的一個分支,研究彈性體由於受外力作用、邊界約束或溫度改變等原因而發生的應力、形變和位移。彈性力學的研究對象是完全彈性體,彈性體是變形體的一種,在外力作用下物體變形,當外力不超過某一限度時,出去外力後,除去外力後物體即恢復原狀。根據問題的性質,忽略一些很小的次要因素,對物體的材料性質採用了一些基本假定,即彈性力學的基本假定,主要有連續性、完全彈性、均勻性、各向同性,符合以上假定的物體,就稱為理想彈性體;此外,假定位移和形變是微小的。物體任意一點的位移,用它在x、y、z三軸上的投影表示。研究討論的平面應力彈性體的形狀為等厚度均勻薄板,厚度方向的尺寸小於其他兩個方向的尺寸。在解決彈性力學平面問題時,需要建立基本方程:平衡方程—應力與外力之間的關係;幾何方程—位移與應變之間的關係;物理方程—應變與應力之間的關係。以及邊界條件的建立,邊界條件表示在邊界上位移與約束,或應力與面力之間的關係式。位移分量已知的邊界,建立位移邊界;給定了面力分量,建立應力邊界條件。聖維南原理,面力的改變,就只會使近處產生顯著的應力改變,而遠處的應力改變可以忽略不計。在解決平面問題時,按位移求解平面以及在問題或按應力求解平面問題。以及在直角坐標和及極坐標中建立基本方程和求解方法,彈性力學的學習中,對應變、應力等量的意義有了更深的了解,以及對量的表示方式有所了解。
彈性力的基本假設
(1)連續性,所有的物理量均可以用連續函式,從而可以套用數學分析的工具;
(2)完全彈性,物體中的應力與應變之間的物理關係可以用胡克定律來表示;
(3)均勻性,物體的彈性常數等不隨位置坐標而變化;
(4)各向同性,彈性常數等也不隨方向而變化;
(5)小變形假定,簡化幾何方程,簡化平衡微分方程。
相關原理
聖維南原理
聖維南原理是基於靜力等效原理,當將面力的等效變換範圍套用到大邊界上,則必然使整個物體的應力狀態都改變,所以大邊界不能套用靜力等效,在大邊界上不能套用聖維南原理。
疊加定理
線上彈性和小變形假定下,作用於彈性體上幾組荷載產生的總效應(應力和變形),等於每組荷載產生的效應之和,且與載入順序無關。
虛位移原理
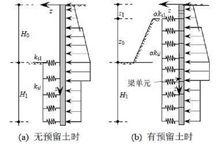 彈性力
彈性力假定處於平衡狀態的彈性體在虛位移過程中,沒有溫度的改變,也沒有速度的改變,既沒有熱能和動能的改變,則按照能量守恆定理,形變勢能的增加,等於外力勢能的減少,也就等於外力所做的功,即所謂虛功。
彈性力的研究方法
在彈性體區域內部,考慮靜力學、幾何學和物理學三方麵條件,分別建立三套方程。即根據微分體的平衡條件,建立平衡微分方程;根據微分線段上形變與位移之間的幾何關係,建立幾何方程;根據應力與形變之間的物理關係,建立物理方程。此外,在彈性體的邊界上還要建立邊界條件。在給定面力的邊界上,根據邊界上微分體的平衡條件,建立應力邊界條件;在給定約束的邊界上,根據邊界上的約束條件建立位移邊界條件。求解彈性力學問題,即在邊界條件下根據平衡微分方程、幾何方程、物理方程求解應力分量、形變分量和位移分量。彈性力學中正應力用σ表示,並加上一個下標字母,表明這個正應力的作用面與作用方向;切應力用τ表示,並加上兩個下標字母,前一個字母表明作用面垂直於哪一個坐標軸,後一個字母表明作用方向沿著哪一個坐標軸。並規定作用在正面上的應力以沿坐標軸正方向為正,沿坐標軸負方向為負。相反,作用在負面上的應力以沿坐標軸負方向為正,沿坐標軸正方向為負。平面應力問題是指很薄的等厚度薄板,只在板邊上受有平行於板面並且不沿厚度變化的面力,同時,體力也平行於板面並且不沿厚度變化。對應的應力分量只有σx ,σy ,τxy 。而平面應變問題是指很長的柱形體,在柱面上受有平行於橫截面並且不沿長度變化的面力,同時體力也平行於橫截面並且不沿長度變化,對應的位移分量只有u 和v。