原理的引入
由於許多力學問題很難用數學方法去解決,必須通過實驗來研究。然而直接實驗方法有很大的局限性,其實驗結果只適用於某些特定條件,並不具有普遍意義,因而即使花費巨大,也難能揭示現象的物理本質,並描述其中各量之間的規律性關係。還有許多現象不宜進行直接實驗,例如飛機太大,不能在風洞中直接研究飛機原型的飛行問題;而昆蟲的原型又太小,也不宜在風洞中直接進行吹風實驗;況且,直接實驗方法往往只能得出個別量之間的規律性關係,難以抓住現象的本質。我們更希望用縮小的飛機模型或放大的昆蟲模型進行研究。那么我們最關心的問題就是從模型的實驗結果所描述的物理現象能否真實再現原來物理現象?如果要使從模型實驗中得到的精確的定量數據能夠準確代表對應原型的流動現象,就必須在模型和原型之間滿足以下的相似性。
相似概述
( 1 )幾何相似
幾何相似是指模型與其原型形狀相同,但尺寸可以不同,而一切對應的線性尺寸成比例,這裡的線性尺寸可以是直徑、長度及粗糙度等。如用下標p和m 分別代表原型和模型,則
線性比例常數可表示為 Cl=lp/lm
面積比例常數可表示為 Ca=Ap/Am=Cl^2
體積比例常數可表示為 Cv=Vp/Vm=Cl^3
( 2 )運動相似
運動相似是指對不同的流動現象,在流場中的所有對應點處對應的速度和加速度的方向一致,且比值相等,也就是說,兩個運動相似的流動,其流線和流譜是幾何相似的。
速度比例常數可表示為 Cv=Vp/Vm;
由於時間的量綱是l/V,因此時間比例常數為 Ct=tp/tm=(lp/Vp)/ (lm/Vm)=Cl/Cv
由此加速度比例常數Ca=ap/am=Cv/Ct=CI/Ct^2
 模型滿足幾何相似、運動相似和動力相似
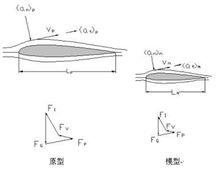
模型滿足幾何相似、運動相似和動力相似( 3 )動力相似動力相似即對不同的流動現象,作用在流體上相應位置處的各種力,如重力、壓力、粘性力和彈性力等,它們的方向對應相同,且大小的比值相等,也就是說,兩個動力相似的流動,作用在流體上相應位置處各力組成的力多邊形是幾何相似的。
一般地說,作用在流體微元上的力有重力Fg、壓力Pp、粘性力Fv、彈性力Fe和表面張力Ft。如果流體是作加(減)速運動,則加上慣性力Fi後,上述各力就會組成一個力多邊形,因此Fg+Fp+Fv+Fe+Ft+Fi=0。
當然,在許多實際問題中,上述各力並非同等重要,有時有些力可能不存在或者小得可以忽略不計,例如Fe和Ft,見圖。如果在滿足幾何相似及運動相似的兩個流動現象中,作用在任何流體微元上的力有Fg、Fp、Fv和Fi等,於是,如果這些力滿足以下條件,則說兩個現象是動力相似的。
動力比例常數可表示為:Cf=Fgp/Fgm= Fpp/Fpm= Fvp/Fvm= Fip/Fim=…
滿足以上相似條件時,兩個流動現象(或流場)在力學上就是相似的。這三種相似條件中,幾何相似是運動相似和動力相似的前提和依據,動力相似是則是流動相似的主導因素,而運動相似只是幾何相似和動力相似的表征;三者密切相關,缺一不可。
相似準則
理論上,任意一個流動由控制該流動的基本微分方程和相應的定解條件唯一確定。兩個相似的流動現象,為了保證它們遵循相同的客觀規律,其微分方程就應該相同,這是同類流動的通解;此外,要求得某一具體流動的特解,還要求其單值條件也必須相似。這些單值性條件包括:
(1)初始條件,指非定常流動問題中開始時刻的流速、壓力等物理量的分布;對於定常流動不需要這一條件。
(2)邊界條件,指所研究系統的邊界上(如進口、出口及壁面處等)的流速、壓力等物理量的分布。
(3)幾何條件,指系統表面的幾何形狀、位置及表面粗糙度等。
(4)物理條件,指系統內流體的種類及物性,如密度、粘性等。
因此,如果兩個流動相似,則作為單值性條件相似,作用在這兩個系統上的慣性力與其它各力的比例應對應相等。在流體力學問題中,若存在上述所有這六種力,而且滿足動力相似,則必須使下列各力間的比例對應相等。
慣性力與壓力(或壓差)之比: Fi/Fp
慣性力與重力之比: Fi/fg
慣性力與摩擦力之比: Fi/Fv
慣性力與彈性力之比:Fi/Fe
慣性力與表面張力之比:Fi/Ft
上述五式式分別引入了五個無量綱數,它們依次是:
1) 歐拉數Eu=2Δp/(ρ·V^2),例如以後經常用到的表示物體表面壓力分布的壓強係數,以及升力係數和阻力係數等。物理上,歐拉數表征了慣性力與壓強梯度間的量級之比。
2) 弗勞德數Fr=V/sqrt (l·g),物理上,弗勞德數表征了慣性力與重力間的量級之比,是一個表征流速高低的無量綱量。
3) 雷諾數Re=Vl/υ,物理上,雷諾數表征了相似流動中慣性力與粘性力間的量級之比,流動的Re數小,表示與慣性力的量級相比,粘性摩擦力的量級要大得多,因此可以忽略慣性力的作用;反之,Re數大則表示慣性力起主要作用,因此可以當作無粘流體處理。
4) 馬赫數Ma=V/c,物理上,馬赫數表征了慣性力與彈性力間的量級之比,是氣體可壓縮性的度量,通常用來表示飛行器的飛行速度或者氣流的流動速度。
5) 韋伯數We, 物理上,韋伯數表征了慣性力與表面張力間的量級之比。
可以看出,Eu、Fr、Re、Ma和We都是無量綱數,在相似理論中稱作 相似準則或者 相似判據,它們是判斷兩個現象是否相似的依據。 因而,彼此相似的現象,其同名相似準則的數值一定相等。反之,如果兩個流動的單值條件相似,而且由單值條件組成的同名相似準則的數值相等,則這兩個現象一定相似。
相似原理詳述
相似第一定理
兩個相似的流動現象都屬於同一類物理現象,它們都應為同一的數學物理方程所描述。流動現象的幾何條件(流場的邊界形狀和尺寸)、物性條件(流體密度、粘性等)、邊界條件(流場邊界上物理量的分布,如速度分布、壓強分布等),對非定常流動還有初始條件(選定研究的初始時刻流場中各點的物理量分布)都必定是相似的。這些條件又統稱為單值條件。如前所述,兩個流動現象力學相似,則在空間對應點和對應的瞬時諸物理量各自互成一定的比例,而這些物理量又必須滿足同一的微分方程組,因此各量的比例係數,即相似倍數,不能是任意的,而是彼此制約的 。
綜上可得到結論: 彼此相似的物理現象必須服從同樣的客觀規律,若該規律能用方程表示,則物理方程式必須完全相同,而且對應的相似準則必定數值相等。這就是相似第一定理。值得指出,一個物理現象中在不同的時刻和不同的空間位置相似準則具有不同的數值,而彼此相似的物理現象在對應時間和對應點則有數值相等的相似準則,因此,相似準則不是常數。
相似第二定理
要使試驗模型同它所模擬的研究對象相似,試驗的結果才能套用到研究對象上去。判斷兩個現象是否相似,往往不能用物理量在對應時間和空間的分布是否保持同一比值來判定。例如,風洞中模型飛機流場與實際飛行著的飛機流場相似問題,往往只知道飛機遠前方的來流速度,飛機附近的流場分布卻不知道,因此不能根據相似定義來判斷二者是否相似。
兩個物理現象相似,必定是同一類物理現象。因此,描述物理現象的微分方程組必定相同,這是現象相似的 第一個必要條件。
單值條件相似是物理現象相似的 第二個必要條件。因為服從同一微分方程組的同類現象有許多,單值條件可以將研究對象從無數多現象中單一地區分出來,數學上則是使微分方程組有唯一解的定解條件。
單值條件中的物理量所組成的相似準則相等是現象相似的 第三個必要條件。
反過來說,屬於同一類物理現象且單值條件相似時,兩個現象才有時間和空間的對應關係以及與時間和空間聯繫的相同物理量,如果對應的相似準則相等,又保持了在對應的時間和空間點上物理量保持相同的比值,也就保證了兩個物理現象的相似。
綜上所述,相似條件可表述為: 凡同一類物理現象,當單值條件相似且由單值條件中的物理量組成的相似準則對應相等時,則這些現象必定相似。這就是相似第二定理,它是判斷兩個物理現象是否相似的充分必要條件。
原理與試驗
相似原理與量綱分析方法解決了模型試驗中的一系列問題。
要進行模型試驗,首先遇到如何設計模型,如何選擇模型流動中的介質,才能保證與原型(實物)流動相似。根據相似第二定理,設計模型和選擇介質必須使單值條件相似,而且由單值條件中的物理量組成的相似準則在數值上相等。
試驗過程中需要測定哪些物理量,試驗數據如何處理,才能反映客觀實質?相似第一定理表明,彼此相似的現象必定具有數值相等的相似準則。因此,在試驗中應測定各相似準則中所包含的一些物理量,並把它們整理成相似準則。
模型試驗結果如何整理才能找到規律性,以便推廣套用到原型流動中去?由Π定理可知,描述某物理現象的各種變數的關係可以表示成數目較少的無量綱Π表示的關係式,各無量綱Π各種不同的相似準則,它們之間的函式關係式亦稱為準則方程式。彼此相似的現象,它們的準則方程式也相同。因此,試驗結果應當整理成相似準則之間的關係式,便可推廣套用到原型中去。
雷諾數相似法
為更好解釋清楚相似原理的套用,下面介紹一種近似模型法:雷諾數相似法
有許多實際流動,它們主要受粘性力、壓力和慣性力的作用。如流體充滿截面的管道流動,由於不存在自由面,因此,沒有表面張力作用,即可不考慮We相似準則;重力不影響流場,故可不考慮Fr相似準則;如果流速與聲速相比很低,則壓縮性影響也可以忽略不計,即不必考慮Ma相似準則。對於繞物體的低速氣流或繞深水中潛艇的流體上的彈性力及相應的水流(這時沒有水面波浪形成)的情況也是這樣。
從力學相似的觀點來看,若兩個流場在對應點作用的同種力方向相同、大小成同一比例,則滿足動力相似。對於僅考慮粘性力、壓力和慣性力這三種力的情況下,要使力三角形相似,只需滿足兩條邊成比例且夾角相等,也就是說,在對應點上模型流動作用的慣性力和粘性力與實物流動作用的慣性力和粘性力成同一比例,因此,只要在對應點滿足雷諾數相等即可。從更具有普遍意義的相似定理來看,兩個流動相似,則相似準則數對應相等,由Π定理得出的相似準則方程式亦相同。在(n-k)個相似準則中,其中(n-k-1)個是獨立相似準則、或稱為決定性相似準則(相當於函式的自變數),一個為非獨立相似準則或非決定性相似準則(相當於函式的因變數)。對於僅考慮粘性力、壓力和慣性力作用的流動情況,將雷諾準則和其它幾何尺寸有關的準則看作獨立準則,歐拉準則為非獨立準則。
在幾何相似的前提下,流動現象相似的決定性準則僅為雷諾準則,則模型試驗必須遵守的相似稱為雷諾相 似。