定義
設函式y=F(x)在區間K:[a,b]上有定義。若在K上有一函式f(x),正數M和正整數r=1/α,使得對K上有任意的x和x+h,有下列不等式:
|F(x+h)-F(x)-f(x)·h|≤M·h^(1+α) ①
或等價的不等式:
|[F(x+h)-F(x)]/h-f(x)|≤M·h^α
則稱F(x)在K上廣義強可導,並稱f(x)是F(x)的導函式,簡稱為F(x)的導數,記作F'(x)=f(x),或y'=f(x),或dy/dx=f(x)。
當r=α=1時稱y=F(x)在K上強可導。
不等式①也可寫成等價的等式形式
F(x+h)-F(x)=f(x)+M(x,h)·h^(1+α) ②
其中M(x,h)在T={P|P=(x,h):x∈K,x+h∈K,h≠0}上有界。
一般的,若K為開區間或半開半閉區間,而y=F(x)在K的任意閉子區間上廣義強可導,則稱F(x)在K上強可導。
強可導的歷史
由牛頓和萊布尼茲創建的微積分,是第一代的微積分。第一代微積分,是說不清楚的微積分。創建者說不清楚,使用微積分解決問題的數學家也說不清楚。微積分的原理雖然說不清楚,其套用仍然在蓬蓬勃勃地發展。微積分就這樣在說不清楚的情形下向前發展了130多年。
由柯西和維爾斯特拉斯等,建立了嚴謹的極限理論,鞏固了微積分的基礎,這是第二代的微積分。第二代的微積分是說清楚了的,但是由於概念和推理繁瑣迂迴,對於絕大多數學習高等數學的學生來說,是聽不明白的微積分。微積分就這樣在多數學習者聽不明白的情形下,又發展了170多年,直到今天。
第三代的微積分,是正在創建發展的新一代的微積分。人們希望微積分不但嚴謹,而且直觀易懂,簡易明快。讓學習者用較少的時和精力就能夠明白其原理,不但知其然而且知其所以然。不但數學家說得清楚,而且非數學專業的多數學子也能聽得明白。
第一代微積分和第二代微積分,在具體計算方法上基本相同。不同的是對原理的說明,前者說不清楚,後者說清楚了。
導數還可以這樣初等化(哲學說清第二代微積分) 應該說無窮小量,起源於微積分學。例如,我們研究二次函式y=x^2的變化率。首先,我們考察y=x^2這一法則下在某一點p(x0,y0)的Δy/Δx。 Δy/Δx=[(x0+△x)^2-x0^2]/△x =[x0^2+2x0△x+△x^2-x0^2]/△x =(2x0△x+△x^2)/△x =(2x0+△x)*(△x/△x) =2x0+△x 現在我們取極限(最終形態),令△x=0:此時我們就有所謂的極限limΔy/Δx=2x0 然而,這種推導在邏輯上是有一個漏洞的。該結論的前提是我們在令△x=0時,依舊堅持△x/△x=1!△x/△x=1的存在則否定了令△x=0的假設,這裡的△x/△x=1絕不會是0/0=1(因為0/0到底是多少無從可知!)。 說白一點就是在推導過程中,先要假設△x≠0,否則就無法把它作為分母,更不能把它約掉從而得出2x0+△x;當我們得出2x0+△x,就立刻出爾反爾的讓△x=0來得到2x0。既然,一開始2x0+△x是在△x≠0的條件下得到的,憑什麼最後又讓△x=0呢! 微積分的創始人之一牛頓,給出的解釋是:“△x是一種無窮小量,無窮小量是一個數變成0之前的最後形態,它的絕對值比任何正數都小。因為△x不是0,所以可以做分母,並可以約掉;又因為△x的絕對值比任何正數都小,所以在2x0+△x中可以忽略不計,於是2x0+△x就等於2x0了。 無窮小量的神秘性在於:它如果是數,數在變成0之前還是數,哪有什麼“絕對值比任何正數都小”的最後形態?如果是數,有何理由能夠像數一樣的運算。 兩種邏輯的交鋒(人的邏輯pk自然界的邏輯): 上面的分析就算是第一種邏輯(人的邏輯)。我們得到了邏輯漏洞,如果要避免漏洞該怎么辦呢?很簡單老老實實的按照數學的規則,順其自然唄: 也就是這樣Δy/Δx=[(x0+△x)^2-x0^2]/△x =(2x0+△x)*(△x/△x) 的式子中令△x=0有Δy/Δx=(2x0+△x)*(△x/△x) =(2x0+0)*(0/0) =0/0(得到這么一種東西!) 事實上我們從形上學的角度,能夠預先知道Δy/Δx在△x=0時,確實是0/0(根本算都不用算!)問題是:0/0有用(實在用途)嗎?而且我們可以把0/0與2x0 2x0當做一回事嗎?即0/0=2x0了(一些人說是不定式,對嗎!) 導數說是研究函式的一種方法,可是我們函式知多少!也許你大約聽過函式的定義(集合上的),可是你知道哲學裡的函式嗎?事情是這樣的:我們說函式是描述運動現象的重要工具,可是運動有什麼重要特徵呢(有運動有什麼)! 物質與運動的辯證關係: 物質是運動的物質,運動是物質的運動。運動是物質的根本屬性和存在方式,物質是運動的主體,物質和運動不可分割。離開物質談運動,或者離開運動談物質,都是錯誤的。 原來是這樣的,有運動必有物質!(自然界的邏輯——運動基本特徵)地球自轉、小貓逮老鼠、移動的衛星……都有物質(地球、貓、老鼠、衛星……)。物理學上為了方便突出物質的存在,於是就把這些物質統一起來(不考慮形狀、大小、性別、顏色、溫度……)叫做質點;用質量來肯定物質的存在,道理也簡單,一切物質皆有質量這樣就可以表示物質的存在了(自然界的邏輯)。 可是要突出物質的存在,只有質量一條路嗎?未必! 物質與空間(絕對空間)的關係 定理I 一切物體總占據著空間且不受影響,並能進行空間交換(這也是自然界的邏輯)。 解釋:事實上這裡的空間指絕對空間,物體占據空間是無條件的,而物體本身又是不受空間影響的。因而物體可以從這個空間到達另一個空間,這便是空間交換。這裡不是指機械運動,而是說明物體能夠運動。 從定義1便可得出物質的幾個自然原理。 物體在絕對空間的原理:1、對空間的占據性。2、不受空間影響性(獨立性)。3、可(空間交換)運動性 談到空間就離不開物質,人們認識空間是通過物質而得以實現的。無論何種物質都會以某種形態出現在空間裡,物質是占據一定空間的存在(這種容納物質的空間叫做物質空間!)。所以,要突出物質的存在物質空間也是一條道路!當然,也可以不考慮物質的形狀、大小、性別、顏色、溫度…… 我們說函式是描述運動現象的理論:是指不關心物質的速度、加速度……只考慮運動空間形態——軌跡(曲線或者直線),大約是說了物質在空間中位置變化方式(機械運動)。由於,函式遇到了運動,而運動又拉著物質、物質又必然引出空間。所以,大約得到了這樣一種自然界的邏輯關係:運動是物質與空間的母體,物質空間是物質與純粹空間的集合。 純粹空間的存在表明空間的本質是空無(數學值相對實體物質定義為0),空間可獨立於物質、意識之外而存在,空間既不是物質,也不是意識。這就是空間的真實性、客觀性和非物質性。物質空間的存在以及與純粹空間的轉換,表明了空無的空間具有包容性。由於是相對定義,這樣描述物質的數學值只能是非0的數了。這樣一種自然界邏輯就有問題了——物質空間!物質空間物質部分>0,空間部分=0,於是搞笑的邏輯提問出現了:有沒有一種數即等於0,又大於0來描述物質空間呢?在人的保守邏輯里,這種邏輯顯然是不合理的(不存在這樣的數),錯誤的邏輯!然而,自然界偏偏就是有這種邏輯,而且是普遍的邏輯並且一定會在運動現象中出現! 微積分如何抓住自然現象本質 數學不是單純的數字遊戲!是有套用價值的,體現在各類數學模型上。數學如果本身,允許這樣的解存在,那么就應該肯定其合理性(尊重自然界的抉擇)。 Δy/Δx=[(x0+△x)^2-x0^2]/△x =[x0^2+2x0△x+△x^2-x0^2]/△x =(2x0△x+△x^2)/△x =(2x0+△x)*(△x/△x) =2x0+△x 現在我們取極限(最終形態),令△x=0:此時有limΔy/Δx=2x0 在令括弧內△x=0(純粹空間的性質)時,堅持括弧外△x/△x=1(物質的性質)雖然,△x/△x=1的存在則否定了△x=0的假設,但這是基於運動基本特徵的必然結果! 而另一方面,Δy/Δx=[(x0+△x)^2-x0^2]/△x =(2x0+△x)*(△x/△x) 的式子中令△x=0有Δy/Δx=(2x0+△x)*(△x/△x) =(2x0+0)*(0/0) =0/0(純粹空間的解) 也可以有,limΔy/Δx=0/0. 同一個表達式,居然有兩個數學解!似乎數學想告訴我們什麼,數也許可以是雙向的,就好像物理學中的:光一樣,具有波粒二象性。 微積分領域,我們遇到了許多所謂的駁論。微積分如果真是錯誤的推導,又何以得出正確的結論呢?Δx/Δx=1,應該理解為物質的比,而Δx=0,則應理解為純粹空間的特性。最後,得到的則是一個物質空間的解。也就是limΔy/Δx=2x0,而limΔy/Δx=0/0則是純粹空間的解。((二元微積分學也適用) 所以,0/0≠2x0(二者的邏輯形式不同),但二者可以同時存在,或者獨立存在!無窮小量其實是自然界的辯證法,它不是一種特殊的數或者說不是數。貝克萊駁論在人的邏輯學裡是一條駁論,而在自然女神眼裡則談不上什麼駁論了。 為什麼導數(物質空間的解)是一條直線的斜率,而不是別的東西?因為,物質運動軌跡是物質在空間中的運動,不因為做曲線或是直線軌跡物質而變化(在任意的位置上,可以選擇直線運動也可以選擇曲線運動),割線越來越短(終點返回起點),物質性來源於割線自然最後的物質也必然是直線!(微觀的線段更合理些吧。) 不過函式是人類頭腦里的運動模型,並非自然界的實在運動,所以不是所有函式都有物質空間的解!函式與物質空間是既不成分也不必要條件,切忌!切忌! 物理學認為:速度是描述物質運動快慢的物理量。我們所關心的是描述能有多高的精度,離自然界真相有多近!微積分中的△t是兩個不同的值,一個為0(靜止的空間),一個非0(運動的物質),於是極限的最後是一個運動物質空間的解(精度最高的解),當然0/0也是一個解(純粹空間的解,不用它);瞬時速度翻譯過來是說:在任意某個純粹空間(畫龍點睛)里正在運動的物質——這是自然界普遍的現象。以後,還要談定積分學.
第三代微積分和前兩代微積分,在具體計算方法上也沒有不同。不同的仍是對原理的說明。
幾十年來,國內外都有人從事第三代微積分的研究以至教學實踐。這方面的努力,已經有了顯著的成效。在我國,林群院士是這個方向的倡導者,他在近十年間在此方向做了大量的工作。
微積分最基本最重要的概念是導數。第一代微積分說不清楚,主要就是導數的概念說不清楚。第二代微積分聽不明白,主要是從導數的概念推導函式的性質聽不明白。學過高等數學的同學都會用“導數正則函式增”的定理解題,但很少有人知道其中的道理。還有泰勒公式,微積分基本定理,多數人知其然不知其所以然。
所以,人們改革微積分,首先從導數概念入手。
在上世紀40年代,有人提出了區間上一致可導的概念。
定義1(一致可導的定義) 設函式F(x)和f(x)都在區間[a,b]上有定義,如果對於[a,b]上任意的x和x+h,一致的有
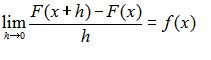
則稱F(x)在區間[a,b]上一致可導,並稱f(x)是F(x)的導函式, 簡稱為F(x)的導數,記作 F'(x)=f(x),或y'=f(x),或dy/dx=f(x)。
可以證明,一致可導等價於連續可導,即F(x)的導數存在並且在[a,b]上連續。但直接採用定義1,給推理帶來了方便。
一致可導的定義,仍然依賴於極限概念。能不能不用極限來定義導數呢?林群指出[2],採用“一致微商”的定義可以大大簡化微積分基本定理的論證。在2005年11月在上海的一次全國性教學研討會上,他進一步闡述了微積分改革的思想;在2006年5月12-14日在西安舉行的“中國高等教育學會教育數學專業委員會學術研討會”上,他又作了題為“新版微積分”的大會報告,在報告中明確提出了作為函式導數初等定義的“一致性不等式”,為微積分的初等化指出了一條新路,其詳細的推導論證見[3]。 林群用一致不等式定義導數的方法,畧加形式化後就是
定義2 (用一致不等式定義導數)設函式F在[a,b]上有定義。如果有一個在[a,b]上有定義的函式f和正數M, 和一個在(0,b-a]上正值遞減無界的函式D(x),使得對[a,b]上任意的 x 和 x+h ,有下列不等式:
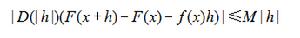
則稱F在[a,b]上一致可導,並且稱f(x)是F(x)的導數, 記作F’(x)= f(x).
將(2)用傳統的記號表示,無非就是
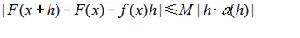
此處a(h)是h→0時的無窮小。而用不等式(2)可以避免無窮小。
可以證明,定義2和定義1是等價的。但是採用定義2就避免了極限概念,可以顯著地簡化推理,提前讓學生掌握微積分的核心知識。
在定義2中取D(x)=1/x,得到所謂強可導或李普西茲可導的定義。
定義3 (強可導的定義) [3][4][5]設函式y=F(x)在I上有定義.如果存在一個定義在I上的函式f(x)和正數M,使得對 I上的任意點x和x+h,(這裡h可正可負) 成立不等式
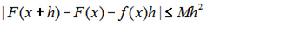
則稱函式y=F(x)在I上強可導(或李普西茲可導),並稱f(x)是F(x)的導數,記做F'(x)=f(x),或y'=f(x),或dy/dx=f(x)。
容易證明,強可導函式的導數差商有界,即滿足李普西茲條件。這是國外有人把它叫做李普西茲可導的由來。
研究表明,在引進實數理論和極限理論之前,就能夠嚴謹地推出一系列微積分的基本定理和計算公式。第3代的微積分理論框架,已經基本形成。
在中高等數學課程中,要求學生會用微積分方法解決一些實際問題。這些套用的理論依據主要是兩條,一條是導數正則函式增,一條是微積分基本定理。這兩條在現在的高中教材中都是不能證明的,甚至在大學裡非數學專業的高等數學教材中也是不要求完整證明的。對如此重要的定理學生只能知其然而不知其所以然,這是高等數學教學中長期未能解決的難題。
當然,極限畢竟是要學的.學了些微積分的基礎知識再學極限,也許更容易理解.因為例子更豐富,更現成了.
微積分入門教學難是被廣泛關注的問題.或許第三代微積分的出現有助於解決這個難題。
有關強可導的評論
西方哲學家繼承了古希臘哲學理性思維的傳統,注重理性思辯和熱衷於構建形上學的理論體系,這種思維方式和習慣與高等數學的思維習慣是相似的。並且西方哲學理論和哲學觀點多是建立在嚴密的邏輯推理和論證的基礎之上的,即使是上帝的存在問題他們也要向對待數學問題那樣試圖用嚴密的辯證法和邏輯來給予證明。西方哲學家的這種注重推理論證和尋求因果聯繫的理性主義的思維習慣一旦與面向感性世界的經驗主義和實驗科學相結合將極大地促進自然科學的發展。
在對於微積分的研究上,西方數學家把眼光放在最細微的地方,雖然他們沒有強調這一點,然微積分確實征服了“點”、“線”、“面”。這是一種“征服文化,”所以牛頓、萊布尼茲、柯西在這種文化的薰陶下,長時間內是不會也不可能去考慮:強可導函式的。
中國傳統哲學自孔子以來就培養了一種深厚的“實用理性精神”,總是同做人即人格修養聯繫在一起,因此有關人性論和修養論的內容最為豐富。哲學家提出任何一種學說都要說明它對做人的意義,都要滿足為政治實踐和道德實踐服務的現實需要,這種純功利主義的思維方式和習慣與西方哲學本身所固有的為學術而學術的思維方式和習慣是大相逕庭的,與要求嚴密推理和論證的數學思維方式也是格格不入的。這種思維方式和習慣不利於或者說阻礙了近代自然科學在中國的興起和發展。
強可導函式,整體上暗中回歸了自然界,這種方法維護人的意識(常量數學)比極限論要強烈的多。邏輯思維上較簡單沒有了駁論和矛盾,有利於學生偷懶。西方的微積分方法,側重於了數學與自然界最終的和諧與統一;中國的初等化微積分側重於數學與人的和諧統一。西方為了研究自然界,犧牲初等數學(意識)了為代價,體現了對自然界的熱愛和尊重。中國的初等化微積分,體現了以人為本的理念。
學習西方哲學,改造中國傳統哲學的思維方式和習慣,養成一種與數學思維方式相似的注重嚴密推理和論證的思維方式和習慣,對於促進我國科學技術的發展是大有裨益的!所以我覺得即便學了初等的微積分,還是有必要重新學極限論的微積分。這不是麻煩,而是思維的轉型。中學一次,大學再學一次!就怕我們的學生,覺得強可導簡單,對西方微積分有牴觸情緒,不願意接受。最好是中西結合,最終的道路都是殊途同歸,不可厚此薄彼。
強可導定義下導數的唯一性證明
對於②式,F(x+h)-F(x)=f(x)+M(x,h)·h^(1+α) ,對α=1時進行證明。
用反證法,設g(x),t(x)都滿足定義中的條件,由②式得:
F(x+h)-F(x)=g(x)h+M(x,h)h^2
F(x+h)-F(x)=t(x)h+N(x,h)h^2
兩式相減得:
0=[g(x)-t(x)]h+[M(x,h)-N(x,h)]h^2
若有u使g(u)-t(u)=d≠0,由於M(x,h)和N(x,h)有界,可知有正數M使得
|dh|=|[g(u)-t(u)]h|≤Mh^2
即|d|≤M|h|,當h<|d/M|時推出矛盾。證閉。
一些常用結論
常數的導數為0:C‘=0
一次函式的導數為常數:(ax+b)'=a
n次函式的導數:(x^n)'=n·x^(n-1)
兩函式之和、差的導數等於兩導數之和、差:(F(x)±G(x))'=F'(x)±G'(x)
函式常數倍的導數等於導數的常數倍:(C·F(x))'=C·F'(x)
兩函式乘積的導數:(F(x)·G(x))'=F'(x)·G(x)+F(x)·G'(x)
兩函式之商的導數:(F(x)/G(x))'=(F'(x)·G(x)-F(x)·G'(x))/( v^2)
