弧長函式

弧長函式(arc length function)，是指量度弧長的函式。設Γ為定義在[a，b]上的可求長曲線，對t∈[a，b]，Γ的參數表示φ對[a，t]的限制所表示的曲線的長度記為L(t)，如此定義的函式L：[a，b]→[0，l]稱為弧長函式，這裡l是Γ的長度，L是嚴格增函式，存在反函式L：[0，l]→[a，b]，複合函式φ°L：[0，l]→R稱為Γ的以弧長為參數的表示，弧長參數以s表示，這樣，Γ有參數方程x=φ(L(s)),s∈[0,l]。每一條可求長曲線都有以弧長為參數的表示，這種表示稱為曲線的自然方程 。

基本介紹

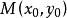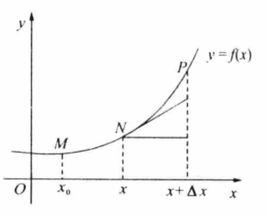
弧長函式

定義 設函式f(x)在區間(a，b)上具有連續導數，曲線y=f(x)在每點處都存在切線，如圖1所示。在曲線y=f(x)上取定一點作為計算弧長的起點，另外任取一點N(x，y)，則從點M到點1N的有向弧長(和弧的長度不同)記為s，它是x的函式，稱為 弧長 函式，記為

弧長函式

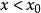弧長函式

弧長函式

我們規定：當點N在點M的右側()時，s為正值；當點N在點M的左側()時，s為負值。所以弧長函式是x的單調增加函式 。

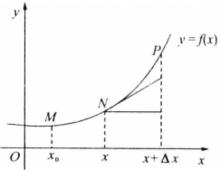圖1

弧長函式的導數和微分

定理1 設函式y=f(x)在[a,b]上連續，在(a，b)內具有一階連續導數，則弧長函式s(x)可微，且

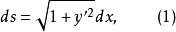弧長函式

則(1)式稱為弧微分公式 。

證明如圖1所示，當橫坐標由x變為x+△x時，它在曲線上對應的點為P，對應於x的增量△x，弧長函式的增量為

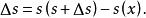弧長函式

弧長函式

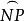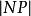弧長函式

當P與N充分接近時，弧的長度△s近似地可以用其所對應的弦NP的長度來代替，如圖1所示，且

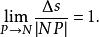弧長函式

因為

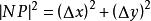弧長函式

或

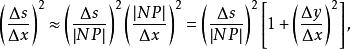弧長函式

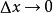弧長函式

當時，上式兩端取極限可得

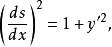弧長函式

因為s(x)是x的單調增加函式，所以取

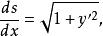弧長函式

由此可得弧長微分公式

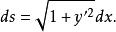弧長函式

如果曲線的方程是由參數方程

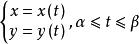弧長函式

或極坐標方程

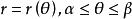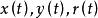弧長函式

弧長函式

給出，且均有連續導數，則分別有弧長微分公式

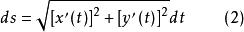弧長函式

和

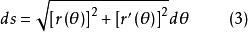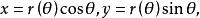弧長函式

弧長函式

(2)式是顯然的，在極坐標的情況下，所以

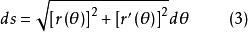弧長函式