定義
將地區平面直角坐標系或建築坐標系與當地高斯平面直角坐標系進行連測後,可以將點的坐標在這兩種坐標系之間進行坐標換算。
空間直角坐標系
解析幾何為了溝通空間圖形與數的研究,需要建立空間的點與有序數組之間的聯繫,為此我們通過引進空間直角坐標系來實現。
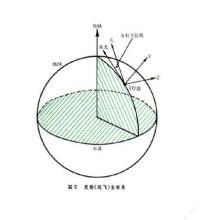
過定點O,作三條互相垂直的數軸,它們都以O為原點且一般具有相同的長度單位.這三條軸分別叫做x軸(橫軸)、y軸(縱軸)、z軸(豎軸);統稱坐標軸.通常把x軸和y軸配置在水平面上,而z軸則是鉛垂線;它們的正方向要符合右手規則,即以右手握住z軸,當右手的四指從正向x軸以π/2角度轉向正向y軸時,大拇指的指向就是z軸的正向,這樣的三條坐標軸就組成了一個空間直角坐標系,點O叫做坐標原點。
判斷方法:在空間直角坐標系中,讓右手拇指指向x軸的正方向,食指指向y軸的正方向,如果中指能指向z軸的正方向,則稱這個坐標係為右手直角坐標系.同理左手直角坐標系。
笛卡爾坐標系
3D數學講解如何在3D空間中精確度量位置、距離和角度,其中使用最廣泛的度量體系是笛卡爾坐標系。笛卡爾坐標系可分2D和3D的,在3D中有兩種完全不同的坐標系:左手坐標系和右手坐標系,左手坐標系是X軸向右,Y軸向上,Z軸向前,右手坐標系的Z軸正好相反,是指向“自己”的,在計算機中通常使用的是左手坐標系,而數學中則通常使用右手坐標系。
多坐標系
遊戲和圖形開發中常用的坐標系有:世界坐標系、物體坐標系、攝像機坐標系、慣性坐標系。 世界坐標系是描述其它坐標系所需要的參考框架,只能用世界坐標系描述其他坐標系的位置,不能用更大的,外部的坐標系來描述世界坐標系。
關於世界坐標系的的典型問題都是關於初始位置和環境的,如:
1、 每個物體的位置和方向。 2、攝像機的位置和方向。 3、世界的每一點的地形是什麼。 4。各物體從哪裡來,到哪裡去。 物體坐標系是和特定物體相關的坐標系。每個物體都有它們獨立的坐標系。 在物體坐標系中可能會遇到的問題: 1、周圍有需要互相作用的物體嗎?(我要攻擊它嗎?) 2、哪個方向,在我前面嗎?我左邊一點?(我應該射擊還是轉身就跑) 攝像機坐標系是和觀察者密切相關的坐標系。是一種特殊的“物體”坐標系。 典型問題: 1、3D空間中的給定點在攝像機前方嗎? 2、3D空間中的給定點在螢幕上還是超出了邊界? 3、某個物體是否在螢幕上?部分還是全部在? 4、兩個物體誰在前面?(可見性檢測,深度排序) 慣性坐標系是為了簡化世界坐標繫到物體坐標系的轉換。從物體坐標繫到慣性坐標系只需旋轉,從慣性坐標繫到世界坐標系只需平移。 嵌套坐標系同樣為了簡化物體在世界坐標系中位置,如一個物體坐標系嵌套一個頭部坐標系,則頭部坐標系可以只與物體坐標系聯繫,簡化操作。
坐標系轉換,套用矩陣表示,一切操作如物體的旋轉、平移過程等都可以用矩陣(4*4齊次空間矩陣)來表示