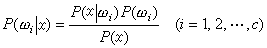昂薩格倒易關係
正文
描述不可逆熱力學過程的線性唯象定律中各係數間的倒易關係。它是粒子微觀運動方程的時間反演不變性在巨觀尺度上的反映。這個關係是1931年由L.昂薩格建立,後經H.B.G.卡西米爾發展,擴充了它的適用範圍。人們常用“流”和“力”來說明不可逆過程。在擴散過程中的物質流密度,熱傳導中的熱流密度,化學反應中的反應速度等都稱為流,用Ji(i=1,2,…,n)表示。引起流的相應力為濃度梯度、溫度梯度、化學親合力等用Xi(i=1,2,…,n)表示。線上性區它們的關係唯象地寫為
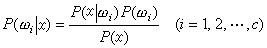
Lij=Lji,
這就是著名的昂薩格倒易關係。這個關係的存在不依賴於具體物質,或具體過程,線上性不可逆過程中具有普遍意義,因而成為線性區非平衡熱力學的主要基礎之一。昂薩格倒易關係套用於實際問題時,得到了很好的驗證。其中對溫差電偶和力熱現象的研究是它成功的突出例證。
溫差電偶效應 用兩種不同金屬A、B焊接形成閉合迴路,人們發現了塞貝克效應、珀耳帖效應、湯姆孫效應(見溫差電現象)。利用昂薩格關係可以證明,塞貝克係數、珀耳帖係數、湯姆孫係數都滿足普遍的關係式,即湯姆孫第一關係
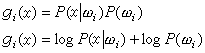
ΠAB=SABT。
而這兩個關係已為實驗證實,所以昂薩格關係的正確性也就得到了證實。費德森效應 實驗發現系統中不同區域的溫度不僅造成熱流,也會引起粒子流
Jn=λ│ΔT│
式中λ 稱為熱力係數。這種效應稱為費德森效應,也叫熱力效應。同時發現壓差不僅引起粒子流,也產生熱流JQ=K│Δp,
式中K稱為力熱係數。利用昂薩格關係可以證明K=λTv,
式中v為物質比容。儘管λ和K 隨物質性質而異,但實驗證實上述關係在不可逆過程的線性區是普遍成立的。配圖
描述不可逆熱力學過程的線性唯象定律中各係數間的倒易關係。它是粒子微觀運動方程的時間反演不變性在巨觀尺度上的反映。這個關係是1931年由L.昂薩格建立,後經H.B.G.卡西米爾發展,擴充了它的適用範圍。人們常用“流”和“力”來說明不可逆過程。在擴散過程中的物質流密度,熱傳導中的熱流密度,化學反應中的反應速度等都稱為流,用Ji(i=1,2,…,n)表示。引起流的相應力為濃度梯度、溫度梯度、化學親合力等用Xi(i=1,2,…,n)表示。線上性區它們的關係唯象地寫為
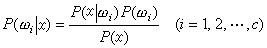
Lij=Lji,
這就是著名的昂薩格倒易關係。這個關係的存在不依賴於具體物質,或具體過程,線上性不可逆過程中具有普遍意義,因而成為線性區非平衡熱力學的主要基礎之一。昂薩格倒易關係套用於實際問題時,得到了很好的驗證。其中對溫差電偶和力熱現象的研究是它成功的突出例證。
溫差電偶效應 用兩種不同金屬A、B焊接形成閉合迴路,人們發現了塞貝克效應、珀耳帖效應、湯姆孫效應(見溫差電現象)。利用昂薩格關係可以證明,塞貝克係數、珀耳帖係數、湯姆孫係數都滿足普遍的關係式,即開爾文第一關係
ΠAB=SABT
和開爾文第二關係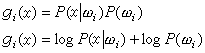 。
。
費德森效應 實驗發現系統中不同區域的溫度不僅造成熱流,也會引起粒子流
Jn=λ│ΔT│
式中λ 稱為熱力係數。這種效應稱為費德森效應,也叫熱力效應。同時發現壓差不僅引起粒子流,也產生熱流JQ=K│Δp,
式中K稱為力熱係數。利用昂薩格關係可以證明K=λTv,
式中v為物質比容。儘管λ和K 隨物質性質而異,但實驗證實上述關係在不可逆過程的線性區是普遍成立的。