平衡不完全區組設計的定義
需滿足條件
將v個水平安排到b個區組中，若滿足以下幾個條件，稱為平衡區組設計：
（1）每個區組包含k個水平一區組大小；
（2）每個水平在r個區組中出現一水平重複數；
（3）每對水平在λ個區組中相遇一相遇數。
若k<v，且B是平衡區組設計，則B是一個平衡不完全區組設計(BIBD)。
參數
平衡不完全區組設計有五個參數：
（1）b：區組數；
（2）v：水平數；
（3）k：在每個區組中水平的個數；
（4）r：包含每個水平的區組的個數；
（5）λ：包含每對水平的區組的個數。
在這裡我們稱b、v、k、r、λ為BIBD的參數。
定義
定義：BIBD的關聯矩陣為v x b階的0-1陣：
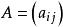平衡不完全區組設計
平衡不完全區組設計關聯矩陣有以下幾個基本性質：
（1）A的每一行和為r；
（2）A的每一列和為k；
（3）A的任意兩行的內積為λ。
BIBD各參數之間的關係及其性質
（1）定理1：在一個BIBD中，每個處理含於r個區組中，其中：
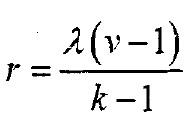平衡不完全區組設計1）推論1：在BIBD中，有bk=vr。
證明：通過行來計算，BIBD的關聯矩陣A中1的個數為6k。通過列來計算，則A中1的個數為vr。因為兩種計數方法的結果相等，所以有bk=vr。
2）推論2：在BIBD中，有λ<r。
證明：根據定義，在BIBD中，有k<v，從而k一1<v一1，使用定理1的結果，λ<r顯然成立。
（2）定理2：Fisher不等式：在一個BIBD中，b≥v。
（3）在一個BIBD中，有參數v=nk、b、r、k和λ，如果b>v+r-1，那么r≥λ+2k。反之也成立。
平衡不完全區組試驗設計的特點
優點
（1）經濟性：
全部試驗水平可以不安排在同一個區組內進行，對區組的要求較低，經濟的解決了試驗成本。
（2）平衡性：
1)每個試驗水平重複次數相同(r相同)；
2)每個區組包含的水平個數相同(k相同)；
3)任意兩個水平對，在整個試驗中出現的重複次數相同(λ相同)。
（3）靈活性：
可以根據k的大小，靈活、分散的進行試驗。
（4）計算的嚴密性：
有嚴格的數學方法有效的消除系統誤差，故試驗精度高。
缺點
平衡不完全設計的缺點是：計算複雜 。
