結合方案
若S={s,s,...,s}為一v元集，且(S×S)\{(s,s)}s∈S}可表為m個兩兩不相交的非空子集R,R,...,R的並，則稱R為結合關係。若諸關係R滿足：
1.每一關係R是對稱的，即當(x,y)∈R時，必有(y,x)∈R。
2.對S中的每個元x，與x有第i種結合關係的元y的個數，即|{y∈S|(x,y)∈R}|川只依賴於i，與x的具體選擇無關，此數記為n。
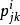部分平衡不完全區組設計
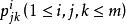部分平衡不完全區組設計3.設x,y有第i種結合關係，則與x有第j種結合關係且與y有第k種結合關係的元z的個數 只依賴於數i，j，k，而與x，y的具體選擇無關，則稱集S連同諸關係R為一個具有m個結合類（或關係）的結合方案。諸數v，n，稱為該結合方案的參數。基集S的元稱為處理。
簡介
部分平衡不完全區組設計是平衡不完全區組設計的一種推廣，簡記為PBIBD。它是基於結合方案的概念，最早由玻色(Bose,R.C.)及內爾(Nair,K.R.)於1939年提出。
設v元集S上有m個結合關係R(1≤i≤m)的結合方案，且S上的一個區組設計有b個區組，若每個區組大小為k，S中任一元恰在r個區組中出現，並且任意兩個有第i種結合關係的元恰同時出現在λ個區組之中，則稱該區組設計是一個具有m個結合類的PBIBD設計。
部分平衡不完全區組設計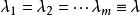
部分平衡不完全區組設計諸數b，v，r，k，λ，n，稱為PBIBD設計的參數。當時，PBIBD設計就是一個(v,k,λ)-PBIBD。
分類
按結合方案的類型，具有兩個結合類的PBIBD設計可分為可分組PBIBD設計、三角形設計、拉丁方型設計等，利用有限域上向量空間以及利用多種有限幾何（辛幾何、酉幾何、正交幾何等）構造結合方案和相應PBIBD設計在中國有比較活躍的研究，它起源於班成的工作，而萬哲先等人則做了較為系統的研究。
套用
在試驗設計中，PBIBD設計被用來安排試驗的方案，其中有兩個結合類且參數較小的PBIBD設計最為有用，它們的存在性及構造已有表可查。結合方案與一類結合的交換代數有關，稱為結合方案的玻色-梅斯納代數，最重要的一類結合方案與編碼理論有關，稱為漢明結合方案。另一類結合方案與強正則圖關係密切，稱為度量方案。此外還有三角形結合方案等其他類型的結合方案。
