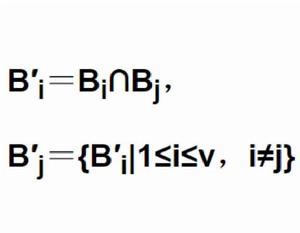基本介紹
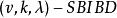 導出設計
導出設計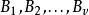 導出設計
導出設計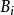 導出設計
導出設計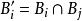 導出設計
導出設計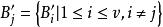 導出設計
導出設計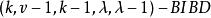 導出設計
導出設計導出設計的具體構作方法如下:若一個 的區組為 ,取定其中一個區組B,對其餘區組 ,記 ,且 ,則 是一個 ,稱這個設計為原對稱設計的一個導出設計 。
相關分析
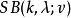 導出設計
導出設計引理1(Ryser)設A是某個 的關聯矩陣且k<v。則
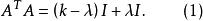 導出設計
導出設計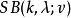 導出設計
導出設計定理2設D=(V B)為一個 。A為其關聯矩陣。則
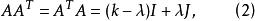 導出設計
導出設計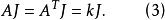 導出設計
導出設計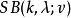 導出設計
導出設計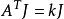 導出設計
導出設計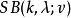 導出設計
導出設計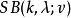 導出設計
導出設計由定理2可得到一系列重要結論,特別由式(1)可知。在一個 中。任意兩個不同區組都恰好包含λ個公共元。再結合等式 可知 的對偶結構也是一個 。
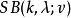 導出設計
導出設計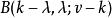 導出設計
導出設計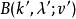 導出設計
導出設計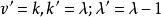 導出設計
導出設計定理3設k<v,若 存在,則 -與 也都存在。此處 。
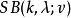 導出設計
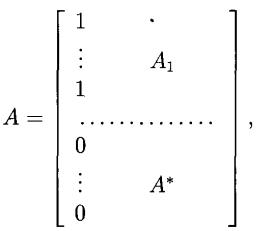
導出設計證設 D=(V, B)P為 ,A為其關聯矩陣,不妨設A的第一列中前k個元素為1,於是可將A作如下分塊:
 導出設計
導出設計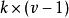 導出設計
導出設計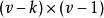 導出設計
導出設計其中A為 矩陣。A*為 矩陣,由式(1)知。A的第一列與其餘各列的內積均為λ,從而A中各列的列和均為λ,A*中各列的列和均為k-λ,由式(2),A中任意兩個不同的行的內積都是λ。因此A中任意不同兩行的內積為λ-1,而A*中任意不同兩行的內積仍為λ,從而
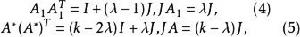 導出設計
導出設計即A為某個B(k',λ';v')的關聯矩陣。而A*則為某個B(k-λ,λ;v-k)的關聯矩陣,這個B(k',λ';v')叫做 D的 導出設計(derived design)。而這個B(k-λ,λ;v-k)叫做 D的剩餘設計(residual design)。
上面給出的構作法。其實就是取定B∈ B。令
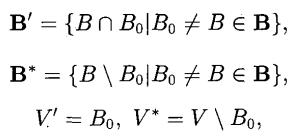 導出設計
導出設計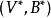 導出設計
導出設計則(V', B')便是 D的導出設計, 便是 D的剩餘設計。
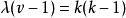 導出設計
導出設計若v,k與λ滿足條件 ,設 D*為一個 B(k-λ,λ;v-k),則稱 D*為一個擬剩餘設計(quasi residual design) 。