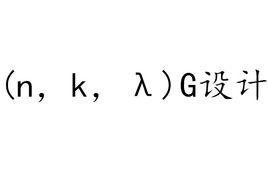基本介紹
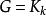 G設計
G設計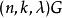 G設計
G設計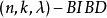 G設計
G設計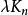 G設計
G設計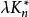 G設計
G設計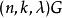 G設計
G設計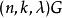 G設計
G設計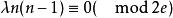 G設計
G設計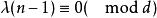 G設計
G設計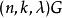 G設計
G設計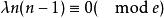 G設計
G設計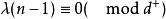 G設計
G設計當 時,一個 設計就是一個 。圖設計可以看成BIBD設計的區組中引入點之間的某種鄰接關係後的推廣,這些同構子圖稱為G區組。當G為有向圖時,將 改為λ重完全有向圖 ,可類似定義 設計。當G為無向圖且 設計存在時, 且 ,式中e是圖G的邊數而d是G的所有頂點度數的最大公因數。當G為有向圖且 設計存在時, , 且
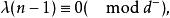 G設計
G設計式中的e是圖G中弧的條數,而d 與d 分別是所有頂點的出度數的最大公因數及入度數的最大公因數。
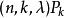 G設計
G設計黑爾(P.Hell)和羅薩(A.Rosa)於1972年首先引入了圖設計這一概念,並研究了 設計的存在性,這裡P表示k個頂點k-1條邊的路,由於圖G的變化千姿百態,G設計的存在性研究面廣量大,已有結果大多是關於路和圈這些簡單而規則的圖G的,只有當k較小時才考察所有可能的圖G,而完整的結果僅限於k=3,4的情形,圖設計的直接構造方法是玻色(R.C.Bose)的對稱重差法的變形,而遞推構造方法則主要利用多部完全圖的分解,與BIBD設計的情形類似,也有可分解性問題以及平衡圖設計問題 。
平衡G設計
平衡G設計是一類特殊的G設計,若在一個G設計中每個頂點在G區組中出現的次數都相同,則稱該圖設計是平衡G設計。當G為正則無向圖(即頂點的度數均相同的圖)或強正則有向圖(即每個頂點的出度數和入度數為同一個常數的圖)時,G設計總是平衡的,平衡G設計的參數除必須滿足一般G設計的必要條件外,還必須滿足進一步的條件:當G為無向圖時,應有
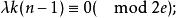 G設計
G設計當G為有向圖時,應有
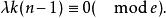 G設計
G設計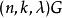 G設計
G設計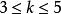 G設計
G設計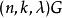 G設計
G設計當G為k個頂點k-1條邊的路或星形圖時,平衡設計存在的必要條件也是充分條件,當且G為無向圖時,平衡設計的存在性也已得到完全解決 。
帶洞G設計
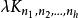 G設計
G設計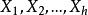 G設計
G設計帶洞G設計亦稱帶洞圖設計,用於遞推構作G設計的一類輔助設計。設是λ重h部無向完全圖,頂點集X劃分為互不相交的,使
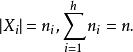 G設計
G設計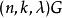 G設計
G設計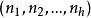 G設計
G設計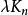 G設計
G設計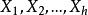 G設計
G設計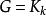 G設計
G設計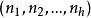 G設計
G設計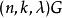 G設計
G設計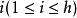 G設計
G設計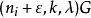 G設計
G設計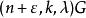 G設計
G設計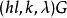 G設計
G設計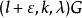 G設計
G設計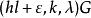 G設計
G設計設G為k個頂點且無孤立點的無向簡單圖,若該多部完全圖能分解成若干個無公共邊的子圖,每一個都與G同構,則稱這樣的分解為一個帶洞設計,稱為其型,這樣的G設計可以看做的通常G設計中帶有一些洞,當時這些洞實際上是可分組設計的組,若每個頂點在G區組中出現的次數相同,則稱這種帶洞圖設計是平衡的,利用帶洞圖設計可以遞推地構造圖設計,若存在型為的帶洞設計,且對每存在設計,其中ε=0或1,則存在設計。特別地,若存在型為(l,l,…,l)的平衡帶洞設計,且存在平衡的設計,其中ε=0或1,則存在平衡的設計,對於有向圖情形,也可類似定義帶洞圖設計概念,並且,有相應的遞推構造圖設計的方法 。