概念
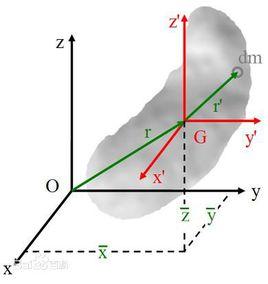
在物理學裡, 垂直軸定理(也叫 正交軸定理)可以用來計算一片薄片的轉動慣量。思考一個直角座標系,其中兩個座標軸都包含與平行於此薄片;如果已知此薄片對於這兩個座標軸的轉動慣量,則垂直軸定則可以用來計算薄片對於第三個座標軸的轉動慣量。
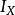 垂直軸定理
垂直軸定理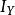 垂直軸定理
垂直軸定理假設OXYZ座標系統的 X-軸與 Y-軸都包含與平行於此薄片,而 Z-軸垂直於薄片的面。 與 分別代表薄片對於 X-軸與 Y-軸的轉動慣量.那么,薄片對於 Z-軸的轉動慣量為
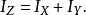 垂直軸定理
垂直軸定理垂直軸定理、平行軸定理、與伸展定則可以用來計算許多不同形狀的物體的轉動慣量 。
證明
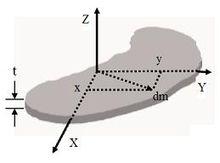 圖1.厚度很薄的薄片
圖1.厚度很薄的薄片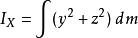 垂直軸定理
垂直軸定理任何實際存在的剛體都有厚度;不可能有零厚度的剛體。參考右圖,假設這剛體是一塊很薄的薄片,厚度 是均勻的,密度也是均勻的。設定薄片的面與 XY-面共平面 。那么,剛體對於 X-軸、Y-軸、與 Z-軸的轉動慣量分別為 ,
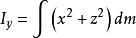 垂直軸定理
垂直軸定理,
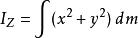 垂直軸定理
垂直軸定理。
由於厚度超小於薄片的面尺寸,我們可以忽略z對於積分的貢獻.因此,
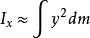 垂直軸定理
垂直軸定理,
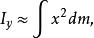 垂直軸定理
垂直軸定理所以,
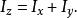 垂直軸定理
垂直軸定理實例
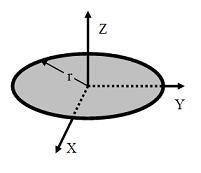 圖1.薄圓盤
圖1.薄圓盤 垂直軸定理
垂直軸定理 垂直軸定理
垂直軸定理a) 如圖2,一個半徑為 ,質量為 的薄圓盤,對於 Z-軸的轉動
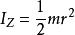 垂直軸定理
垂直軸定理慣量為 。
所以,對於X-軸與 Y-軸的轉動慣量是
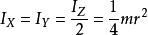 垂直軸定理
垂直軸定理。
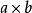 垂直軸定理
垂直軸定理 垂直軸定理
垂直軸定理b) 如圖3,一個尺寸為 ,質量為 的長方形薄片,
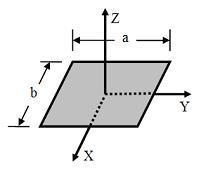 圖2.長方形薄片
圖2.長方形薄片對於 X-軸、Y-軸、與 Z-軸的轉動慣量分別為
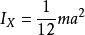 垂直軸定理
垂直軸定理,
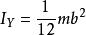 垂直軸定理
垂直軸定理,
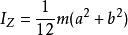 垂直軸定理
垂直軸定理。
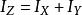 垂直軸定理
垂直軸定理很明顯地, 。
套用
與平行軸定理、伸展定則一樣, 垂直軸定理可以用來計算許多不同形狀的物體的轉動慣量。
1.剛體的一般性垂直軸定理為求三度剛體,特別是圓柱體和旋轉體的轉動慣量提供了一種簡單而又有力的計算工具。對於軸向轉動慣量已知的旋轉體,為求橫向轉動慣量,該定理總是最簡單的計算程式。
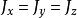 垂直軸定理
垂直軸定理2.對於正多面體,只要當由對稱性使得時,剛體的一 般性垂直軸定理提供的計算程式也是最簡單的 。
相關知識
•平行軸定理
•轉動慣量