定義
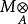 平坦模
平坦模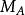 平坦模
平坦模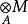 平坦模
平坦模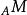 平坦模
平坦模定義1 平坦模是一類重要的模。右A模M,若函子-是正合的,則稱是 平坦模。類似地,對左A模M,若函子-正合,則稱是平坦模。投射模一定是平坦模,反之不一定成立。環A上每個左A平坦模是投射模的充分必要條件是,環A是左完全環 。
 平坦模
平坦模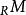 平坦模
平坦模定義2-模叫作平坦的,若對每個單同態
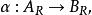 平坦模
平坦模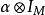 平坦模
平坦模映射也是單同態。
相關性質定理
推論1平坦模的同構像也是平坦的。
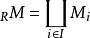 平坦模
平坦模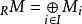 平坦模
平坦模 平坦模
平坦模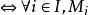 平坦模
平坦模定理2令(或),則有:是平坦的是平坦的。
定理3每個投射模都是平坦的。
 平坦模
平坦模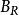 平坦模
平坦模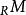 平坦模
平坦模引理4設有-模和,
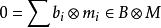 平坦模
平坦模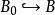 平坦模
平坦模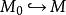 平坦模
平坦模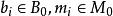 平坦模
平坦模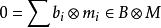 平坦模
平坦模(1) 若,則存在有限生成子模與()使得。
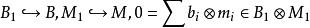 平坦模
平坦模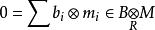 平坦模
平坦模(2)設,則。
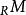 平坦模
平坦模推論5 設是一個模且使它的每個有限生成子模包含在一個平坦子模內,則M是平坦的。
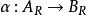 平坦模
平坦模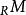 平坦模
平坦模推論6若對一個同態和一個模,
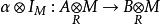 平坦模
平坦模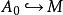 平坦模
平坦模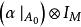 平坦模
平坦模不是單同態,則存在有限生成子模使得也不是單同態。
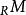 平坦模
平坦模定理7對模,下列敘述是等價的:
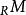 平坦模
平坦模(1)是平坦的;
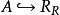 平坦模
平坦模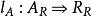 平坦模
平坦模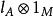 平坦模
平坦模(2) 對每個有限生成右理想,及包含映射,則是單同態;
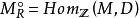 平坦模
平坦模(3)是內射的。
 平坦模
平坦模定理8對於環,下列條件是等價的:
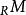 平坦模
平坦模(1) 每個模是平坦的;
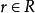 平坦模
平坦模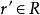 平坦模
平坦模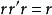 平坦模
平坦模(2) 對每個元素,存在一個元素使得;
 平坦模
平坦模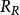 平坦模
平坦模(3)的每個循環右理想是的直和項;
 平坦模
平坦模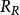 平坦模
平坦模(4)的每個有限生成有理想是的直和項。
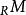 平坦模
平坦模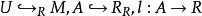 平坦模
平坦模引理9 令是平坦的,表示包含映射,則下列是等價的:
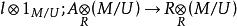 平坦模
平坦模(1)是單同態;
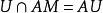 平坦模
平坦模(2)。
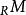 平坦模
平坦模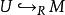 平坦模
平坦模定理10令是平坦的,,則下列是等價的:
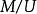 平坦模
平坦模(1)是平坦的;
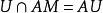 平坦模
平坦模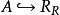 平坦模
平坦模(2)對每個有限生成理想成立。
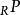 平坦模
平坦模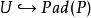 平坦模
平坦模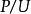 平坦模
平坦模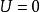 平坦模
平坦模定理11令是投射的,,如果是平坦的,則。
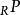 平坦模
平坦模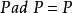 平坦模
平坦模 平坦模
平坦模推論12令是投射模,且,則。

