定義
在統計中,如果要反映出所有原數據間的差異,就要在各原數據之間進行差異比較,當原數據較多時,進行兩兩比較就很麻煩,因此需要找到一個共同的比較標準,取每個原數據值與標準值進行比較。這個標準值就是算數平均數。
平均偏差就是每個原數據值與算數平均數之差的絕對值的均值,用符號A.D.(average deviation)表示。平均偏差是一種平均離差。離差是總體各單位的標誌值與算術平均數之差。因離差和為零,離差的平均數不能將離差和除以離差的個數求得,而必須將離差取絕對數來消除正負號。
平均偏差是反映各標誌值與算術平均數之間的平均差異。平均偏差越大,表明各標誌值與算術平均數的差異程度越大,該算術平均數的代表性就越小;平均偏差越小,表明各標誌值與算術平均數的差異程度越小,該算術平均數的代表性就越大。
平均偏差又有簡單平均偏差和加權平均偏差之分。
計算
簡單平均偏差
如果原數據未分組,則計算平均偏差的公式為:
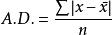 平均偏差
平均偏差該式稱為簡單平均偏差。
加權平均偏差
在分組情況下,平均偏差的計算公式為:
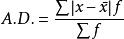 平均偏差
平均偏差該式稱為加權平均偏差。

