基本恆等式
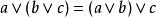 布爾代數恆等式 布爾代數恆等式 |  布爾代數恆等式 布爾代數恆等式 | 結合律 |
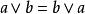 布爾代數恆等式 布爾代數恆等式 | 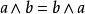 布爾代數恆等式 布爾代數恆等式 | 交換律 |
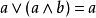 布爾代數恆等式 布爾代數恆等式 |  布爾代數恆等式 布爾代數恆等式 | 吸收律 |
 布爾代數恆等式 布爾代數恆等式 | 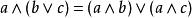 布爾代數恆等式 布爾代數恆等式 | 分配律 |
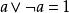 布爾代數恆等式 布爾代數恆等式 | 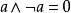 布爾代數恆等式 布爾代數恆等式 | 互補律 |
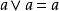 布爾代數恆等式 布爾代數恆等式 | 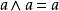 布爾代數恆等式 布爾代數恆等式 | 冪等律 |
 布爾代數恆等式 布爾代數恆等式 | 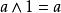 布爾代數恆等式 布爾代數恆等式 | 有界律 |
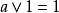 布爾代數恆等式 布爾代數恆等式 | 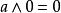 布爾代數恆等式 布爾代數恆等式 | |
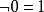 布爾代數恆等式 布爾代數恆等式 | 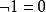 布爾代數恆等式 布爾代數恆等式 | 0和1是互補的 |
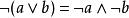 布爾代數恆等式 布爾代數恆等式 | 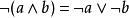 布爾代數恆等式 布爾代數恆等式 | 德·摩根定律 |
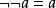 布爾代數恆等式 布爾代數恆等式 | 對合律 |
恆等式
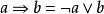 布爾代數恆等式
布爾代數恆等式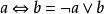 布爾代數恆等式
布爾代數恆等式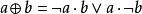 布爾代數恆等式
布爾代數恆等式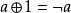 布爾代數恆等式
布爾代數恆等式布爾函式恆等式
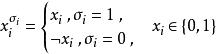 布爾代數恆等式
布爾代數恆等式