巴俾涅原理
正文
在光的衍射中,結構互補的一對衍射屏,在同一場點所產生的兩個衍射場(復振幅)之和,等於自由傳播時該點的光場。巴俾涅原理給出兩個互補屏產生的衍射場之關係稱巴俾涅關係,它可由衍射積分公式直接導出。如圖,設孔型屏∑1造成的衍射場為堚1(P),其互補屏∑2造成的衍射場為堚2(P),而光波通行無阻∑0面的光場為堚0(P),則 ,
,
故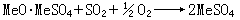
因此,只要兩個互補屏的照明條件不變,對後場任意一點,不論是近場點還是遠場點,巴俾涅關係都是成立的。巴俾涅原理的價值在於,一旦已經求得某屏的衍射場,利用巴俾涅原理便可求得其互補屏的衍射場,這是因為自由光場堚0(P)總是容易事先知道的。
據此,知道了圓孔的衍射場,就能方便地求得圓屏的衍射場;知道了單縫的衍射場,就能方便地求得細絲的衍射場;諸如此類。巴俾涅原理用來處理夫琅和費衍射問題特別有效,因為此時的自由光場除幾何像點外處處為零,所以這些地方的場堚1(P)=-堚2(P),衍射強度I1(P)=I2(P),而在幾何像點處,兩個互補屏的衍射光強應該都是亮點,但光強值可能不同。
因此,兩個互補屏的夫琅和費衍射圖樣看起來完全相同。需要強調指出:巴俾涅原理給出的三個場之關係是復振幅關係,其中位相差要起作用而不是三者光強之關係,不能認為一屏的衍射強度在某處若是亮的,互補屏的衍射強度在該處一定是暗的。
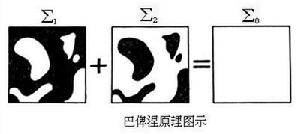 巴俾涅原理
巴俾涅原理1:光的衍射
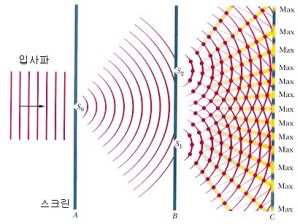 示意圖
示意圖光在傳播過程中遇到障礙物時發生的偏離幾何光學傳播規律的現象.光的衍射也稱作光的繞射,就是光可以“繞過”某些障礙物而在某種程度上傳播到障礙物的幾何陰影區.同時,衍射也使得幾何照明區內出現某些暗斑或暗紋
2:牛頓環
一種等厚干涉條紋.牛頓於1675年觀察到這種干涉條紋.他把一曲率半徑很大的平凸透鏡的凸面放在一塊平板玻璃上,在兩者之間形成以接觸點為中心厚度逐漸增大的空氣膜,膜上等厚度點的軌跡是一組以接觸點為中心的同心3:白光條紋
白光(或可見光)的干涉條紋.白光的有效波長範圍從大約40埃伸展到大約70埃,且各種波長的光有一定組成比例.只有當對可見光區所有波長光的光程差等於零或數倍于波長時,才能觀察到白光的干涉條紋.在楊氏干涉實驗
4:等厚干涉條紋
定域在楔形板附近,與板的等厚度線一致的干涉條紋.它是一種利用分振幅方法產生的干涉現象.當所研究的是折射率n均勻而夾角α又很小的楔形薄板時,如果光源距板較遠或觀察干涉條紋用的儀器的孔徑很小。
5:等傾干涉條紋
一種套用分振幅方法產生的干涉現象.平行平面板在擴展單色光源照明下於無限遠處(透鏡的焦平面上)所產生的干涉條紋,這種干涉條紋是由有相同入射角的光形成的.平面板可理解為受兩個表面限制而成的一層透明物質,
6:楊氏干涉實驗
分波面法雙光束干涉實驗之一.英國物理學家T楊於1802年首先從實驗上研究了光的干涉現象,其中較F早期的是雙孔干涉實驗.這個實驗方法是:用強光照明針孔S,以它作為點光源送出球面波。
7:光的干涉
兩束(或多束)光波在空間疊加後,產生的光強分布與原來兩束(或多束)光的強度之和不同,而出現明暗相間的現象.由於衍射也會造成明暗相間的條紋,因此當若干束光波在空間某一區域相遇而發生干涉時。
8:應力雙折射
又稱光彈性效應.透明的各向同性的介質在壓力或張力的作用下,折射率特性會發生改變,從而顯示出光學上的各向異性.若介質本來就是各向異性晶體。
9:泡克爾斯效應
某些晶體的雙折射與外加電場強度成正比的電光效應.在強電場的作用下,本來是各向同性的介質也可以產生雙折射現象;而本來有雙折射性質的晶體,其雙折射性質也要發生變化。
10:法拉第效應
又稱磁致旋光.在處於磁場中的均勻各向同性(非旋光性)媒質內,線偏振光束沿磁場方向傳播時,振動面發生旋轉的現象.法拉第於1845年發現在強磁場中的玻璃產生這種效應,以後發現其它非旋光性的固、液、氣態物質都有這...更多
