基本介紹
定理1 設1≤λ<k<v-1,n=k-λ,若(v,k,λ)-差集存在。則
(i) λ(v-1)=k(k-1),
(ii)4n-1≤v≤n +n+1。
(iii)當v為偶數時,n為平方數;當v為奇數時。不定方程
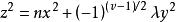 平面差集
平面差集有不全為零的整數解x,y,z。
定義 λ=1時的差集即(v,k,1)-差集叫做 平面差集(planar difference set)。這是因為此時由n=k-λ=k-1及定理1(i)得v=n +n+1,k=n+1,即由此差集可得到一個n階射影平面 。
相關結論
由Singer定理即得下述結果。
定理2 若q為素數冪,則(q +q+1,q+1,1)-循環平面差集存在。
猜想1 所有Abel平面差集都是循環平面差集。
上述猜想尚未獲得解決。又由於所有已知的平面差集都是素數冪階的,因此有理由懷疑非素數冪階平面差集的存在性。即有下述猜想。
若存在n階平面差集,則n必為素數冪。
由定理2可知,在λ=1即平面差集的情形,存在無窮對整數(v,k)使(v,k,1)-循環差集存在,從而也就有無窮多對整數(v,k)使(v,k,1)-Abel差集存在,但對給定的λ≥2已知(v,k,λ)-Abel差集存在的整數對(v,k)都是很稀少的,例如對λ=2,Dickey與Hughes證明了當k≤5000時使(v,k,2)-Abel差集存在的(v,k)僅有4對:
(v,k)=(7,4),(11,5),(16,6)與(37,9).
猜想:對給定的λ≥2,僅有有限對整數(v,k)使(v,k,λ)-Abel差集存在 。
H.A.Wilbrink(1985)和其他一些人觀察到對n>2且n=2(mod 4)的n值,不存在平面差集,見定理3。
定理3 設D是階為v:=n +n+1的交換群G中的一個(n +n+1,n+1,1)-差集,如果n≡0(mod 2)但n≠0(mod 4),則n=2。如果n≡0(mod 3)但n≠0(mod 9),則n=3。