基本介紹
 對角化
對角化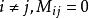 對角化
對角化 對角化
對角化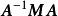 對角化
對角化 對角化
對角化 對角化
對角化對角矩陣是指只有主對角線上含有非零元素的矩陣,即,已知一個n×n矩陣 ,如果對於 ,則該矩陣為 對角矩陣。如果存在一個矩陣 ,使 的結果為對角矩陣,則稱矩陣 將矩陣 對角化。對於一個矩陣來說,不一定存在將其對角化的矩陣,但是任意一個n×n矩陣如果存在n個線性不相關的特徵向量,則該矩陣可被對角化 。
相關定理
 對角化
對角化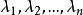 對角化
對角化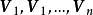 對角化
對角化 對角化
對角化定理1 令 為n×n矩陣,其特徵值為 ,特徵向量為 ,形成線性無關集合,以每個特徵向量為列構成矩陣 ,如下所示。
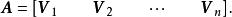 對角化
對角化 對角化
對角化 對角化
對角化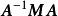 對角化
對角化 對角化
對角化矩陣 可以將矩陣 對角化,乘積矩陣 的主對角元素是矩陣 的特徵值:
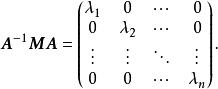 對角化
對角化 對角化
對角化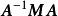 對角化
對角化 對角化
對角化 對角化
對角化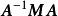 對角化
對角化 對角化
對角化反之,如果存在可逆矩陣 ,使 為對角矩陣,則矩陣 的列等於矩陣 的特徵向量, 的主對角元素為矩陣 的特徵值 。
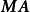 對角化
對角化 對角化
對角化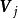 對角化
對角化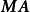 對角化
對角化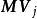 對角化
對角化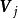 對角化
對角化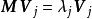 對角化
對角化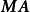 對角化
對角化證明:首先計算矩陣乘積 。由於矩陣 的第j列對應特徵向量 ,則的第j列等於 。由於為特徵向量,則,矩陣乘積可寫為
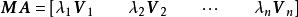 對角化
對角化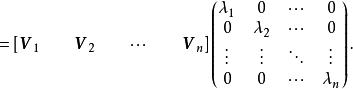 對角化
對角化 對角化
對角化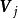 對角化
對角化 對角化
對角化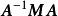 對角化
對角化由於特徵向量線性無關,矩陣可逆,的表達式可寫為
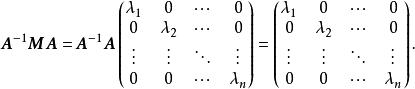 對角化
對角化 對角化
對角化 對角化
對角化 對角化
對角化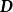 對角化
對角化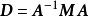 對角化
對角化 對角化
對角化反之,也可證明,可將矩陣對角化的可逆矩陣 必定由的特徵向量組成。假設為n×n對角矩陣,且,其中 為n×n矩陣,有
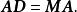 對角化
對角化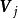 對角化
對角化 對角化
對角化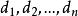 對角化
對角化令表示矩陣 的第j列,為矩陣 D的主對角線上的元素,則矩陣乘積 AD的表達式如下:
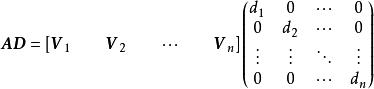 對角化
對角化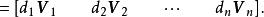 對角化
對角化另,矩陣乘積 MA如下:
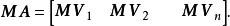 對角化
對角化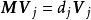 對角化
對角化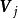 對角化
對角化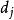 對角化
對角化令 AD的第j列等於 MA的第j列,則,因此是與特徵值對應的矩陣 M的特徵向量。 證畢。
 對角化
對角化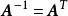 對角化
對角化由於對稱矩陣 M的特徵向量是正交的,則以 M的單位長度的特徵向量為列構成的矩陣 是正交矩陣,因此。由對稱矩陣 M的特徵值組成的矩陣 D的表達式如下 :
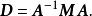 對角化
對角化對角矩陣
定義
對角矩陣(diagonal matrix)是一個主對角線之外的元素皆為0的矩陣。對角線上的元素可以為0或其他值。對角線上元素相等的對角矩陣稱為數量矩陣;對角線上元素全為1的對角矩陣稱為單位矩陣。
(1)對角矩陣形如:
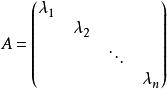 對角化
對角化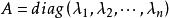 對角化
對角化(2)對角矩陣可以記作:。
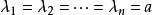 對角化
對角化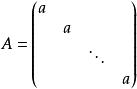 對角化
對角化(3)當時,對角陣稱為數量矩陣。
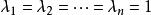 對角化
對角化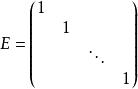 對角化
對角化(4)當時,叫做單位矩陣,記作E,有。
運算規律
和差運算
同階對角陣的和、差仍是對角陣,有:
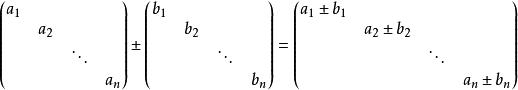 對角化
對角化數乘運算
數與對角陣的乘積仍為對角陣,有:
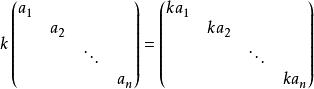 對角化
對角化乘積運算
同階對角矩陣的乘積仍為對角陣,且它們的乘積是可交換的,有:
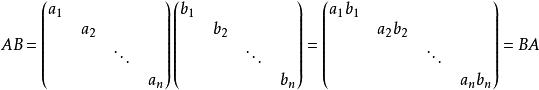 對角化
對角化矩陣相似於對角矩陣的條件
充要條件
n階矩陣A相似於對角矩陣的充要條件是A有n個線性無關的特徵向量。
證明過程:
(1)必要性。
設有可逆矩陣P,使得
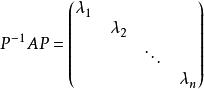 對角化
對角化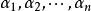 對角化
對角化令矩陣P的n個列向量為,則有
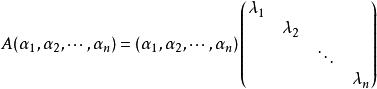 對角化
對角化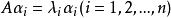 對角化
對角化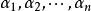 對角化
對角化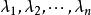 對角化
對角化因而,因為P為可逆矩陣,所以為線性無關的非零向量,它們分別是矩陣A對應於特徵值的特徵向量。
(2)充分性。
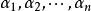 對角化
對角化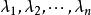 對角化
對角化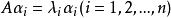 對角化
對角化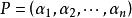 對角化
對角化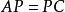 對角化
對角化由必要性的證明可見,如果矩陣A有n個線性無關的特徵向量,設它們為,對應的特徵值分別為,則有,以這些向量為列構造矩陣,則P可逆,且,其中C如下:
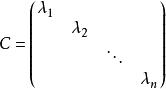 對角化
對角化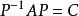 對角化
對角化即。
推論
若n階矩陣A有n個不同的特徵值,則A必能相似於對角矩陣。
說明:當A的特徵方程有重根時,就不一定有n個線性無關的特徵向量,從而未必能對角化。

