對數恆等式的形式
在對數中,存在這樣一個恆等式:在a>0且a≠1,N>0的情況下,a^(Log aN)=N;即:
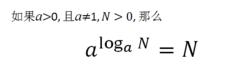 對數恆等式
對數恆等式對數恆等式的證明
在a>0且a≠1,N>0時
設:Log aN=t,(t∈R)
則有a^t=N;
a^(Log aN)=a^t=N;
證畢
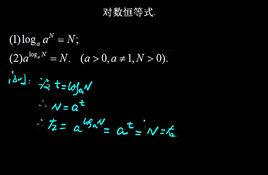
對數恆等式,指的是在對數中,存在一個恆等式。在a>0且a≠1,N>0的情況下,a^(Log)=N;
在對數中,存在這樣一個恆等式:在a>0且a≠1,N>0的情況下,a^(Log aN)=N;即:
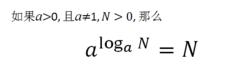 對數恆等式
對數恆等式在a>0且a≠1,N>0時
設:Log aN=t,(t∈R)
則有a^t=N;
a^(Log aN)=a^t=N;
證畢
恆等式(identities),數學概念,恆等式是無論其變數如何取值,等式永遠成立的算式。恆等式成立的範圍是左右函式定義域的公共部分,兩個獨立的函式卻各...
例子 相關聯繫 著名恆等式 乘法公式類 函式類恆等式對數式(logarithmic expression)是一類特殊的解析式,指含有對未知數進行對數運算的解析式,如log2(x-1),logax+b都是關...
基本概念 相關性質 例題解析對數是中學初等數學中的重要內容,是一種計算特殊多位數之間乘積的方法。若a^n=b(a>0且a≠1) 則n=log(a)(b)如果b^n=x,則記n...
歷史 符號 定義 方程式 對數函式0,且a≠1),則x叫做以a為底N的對數,記做x=log(a)(N),其中a要寫於log右下。其中a叫做對數的底,N叫做真數。通常我們將以10為底的對數...
性質 運算法則 換底公式 推導公式 求導數對數式里 a 0,或=1 的時候是會有相應b的值。但是,根據對數定義:log以a為底a的對數;如果a=1或=0那么log以a為底a的對數就可以等於...10為底的對數叫常用對數(common logarithm),並把...
簡介 實際套用 產生歷史 函式性質 公式推導對數的歷史 納皮爾.J. 16、17世紀之交,隨著天文、航海、工程...而發明了對數.對數的發明是數學史上的重大事件,天文學界更是以近乎狂喜的心情迎接這一發明。恩格斯曾經把對數的發明和解析幾何的創始、微積分的建立稱為...
對數的歷史 對數符號 對數的定義 對數函式 複變函數)多項式恆等式的證明一般恆等式(238―256)對稱恆等式(257―260)條件恆等式(261―280)(7)多項式可約性的證明一般可約性的證明...)(6)分式恆等式的證明一般恆等式(341―344)條件恆等式(345...
作品目錄角度都以弧度來度量)。我們可以接著使用泰勒級數的理論來證明下列恆等式對於所有實數 x 都成立 :這些恆等式經常被用做正弦和餘弦函式的定義。它們經...上述恆等式,如果考慮在複平面中eix所定義的單位圓,同上面一樣,我們可以...
概述 基本函式 少用函式 歷史 直角三角定義七、對數換底公式的變形及套用1.換底公式2.換底公式的套用八、指數對數恆等式的證明及套用1.證明指數對數恆等式2.恆等式的套用九、對數式大小的比較方法1.利用單調性2.藉助中間值...
內容簡介 圖書目錄