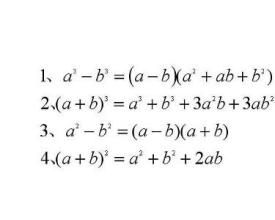定義
完全立方和公式是指兩數和的立方等於這兩個數的立方和與每一個數的平方乘以另一個數3倍的和。
完全立方和公式
(a+b)^3 = a^3+ 3a^2b + 3ab^2 + b^3;
解題時常用它的變形: (a+b)^3 = a^3+ b^3+ 3ab(a+b)和a^3+ b^3= (a+b)^3- 3ab(a+b)
不要小看了這個變形。如果你對這個變形非常熟悉,有“感覺”,在做化簡求值時很有用。例如:
[ (x-y)× (√x+√y) + 3(x√y-y√x) ] / (x√x+y√y)
=[ (√x-√y) + 3√xy × (√x-√y) ] / (x√x+y√y)
=(x√x-y√y) / (x√x+y√y)
完全立方公式分解
分解步驟如下:
(a+b)^3=(a+b)(a+b)(a+b) = (a^2+2ab+b^2)(a+b)=a^3+3a^2b + 3ab^2+ b^3
推廣:
(x1+x2+x3……+xn)*(x1+x2+x3……+xn)^2
=(x1+x2+x3……+xn)*(x1^2+x2^2+x3^2……+xn^2+2x1x2+2x1x3+......+2x(n-1)xn)
=x1^3+x2^3+x3^3+……+xn^3+3x1^2x2+3x2^2x1+……+3[x(n-1)]^2xn.