定義
設有函式系
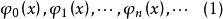完備系
完備系
完備系如果對於任意一個平方可積函式，其按函式系（1）式展開的傅立葉級數為，如果總能使貝塞爾不等式中的等號成立，即
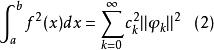完備系則稱此函式系（1）為 完備系，（2）式稱為此函式系的 完備條件，也稱為帕色伐等式。
舉例
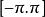完備系定義在上的基本三角函式系
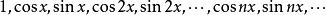完備系是完備系。
重要定理
對於完備系，可以得到以下重要推論。
完備系定理1 如果函式系（1）是完備系，則不會有不恆為零且與此函式系中所有函式正交的連續函式存在。
注 順便提及，有一些書中把本定理的結論作為完備系的定義，而把等式（2）式稱為 封閉方程。
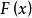完備系 完備系
完備系 完備系定理2 設和都是平方可積函式，其按函式系（1）式展開的傅立葉級數分別為和，若已知函式系（1）是完備系，則有
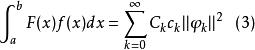完備系 完備系定理3函式系（1）為完備系的充分必要條件：對任意一個平方可積函式，下列等式成立：
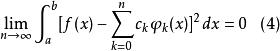完備系 完備系注 本定理可以敘述為：函式系（1）為完備系的充分必要條件是：任意一個平方可積函式的傅立葉級數均值收斂於它本身。
判斷準則
完備系 完備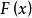系
完備系完備系的判斷準則：如果對於在上連續的一切函式，對任意的，都存在多項式
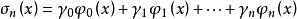完備系使
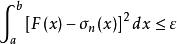完備系成立，則系（1）是完備的。
事件的完備性
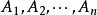完備系
完備系假定我們有這樣的（任意數）個事件，在每個單一作業中必定出現這些事件中的一個，而且只有一個，我們商定這樣一組事件叫做 完備系。很顯然，任何一對對立事件都會構成完備系。
註：構成完備系的事件的機率之和為1.
