概念解釋
奇異邊界法是與基本解法相對應的一種邊界型無格線數值離散方法。該方法提出了源點強度因子的概念,克服了傳統基本解方法中最複雜最頭疼的虛擬邊界問題。基於邊界元法中處理奇異積分的數值處理技術, 導出了源點強度因子的解析表達式, 提出了改進的無格線奇異邊界法, 並進一步將該方法套用於三維位勢問題。該方法消除了傳統方法中樣本點的選取, 在不增加計算量的前提下, 極大地提高了奇異邊界法的計算精度與穩定性。
基本原理
奇異邊界法的近似格式
本文以二維Helmholtz方程為例描述奇異邊界法的基本技術路線:
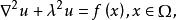 奇異邊界法
奇異邊界法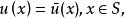 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法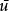 奇異邊界法
奇異邊界法其中 是待求未知量, 為波數, 是空間坐標, 和 分別代表計算域及其邊界, 和 為已知函式。二維Helmholtz方程的基本解是
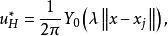 奇異邊界法
奇異邊界法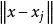 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法這裡 代表 和 兩點間的歐幾里得距離。
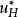 奇異邊界法
奇異邊界法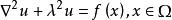 奇異邊界法
奇異邊界法根據基本解法的原理,以基本解 為插值基函式,Helmholtz方程 的待求函式可以近似為
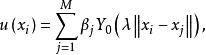 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法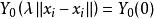 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法其中 是邊界離散點的數目, 為待求插值係數。當配點 和源點 重疊時, 不存在,即產生原點奇異性。為了避免基本解的奇異性,基本解方法的策略是將源點 虛擬地布置在物理域以外的虛假邊界上,而將配點 布置在真實的物理邊界上,即插值源點和配點是兩組完全不同的點。但到目前為止,對於複雜幾何域或多連通幾何域問題,如何較好地布置虛擬源點 以保證計算結果可靠和穩定收斂,仍是基本解方法中一個未能解決的關鍵問題。
 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法奇異邊界法不同於基本解方法的關鍵之處在於,插值源點 和配點 是同一組物理邊界的離散點,因而不存在基本解方法中的虛假邊界選取問題。奇異邊界法的插值公式為:
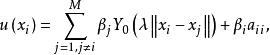 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法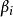 奇異邊界法
奇異邊界法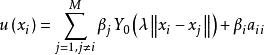 奇異邊界法
奇異邊界法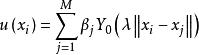 奇異邊界法
奇異邊界法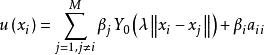 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法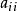 奇異邊界法
奇異邊界法這裡 是插值點的總數, 是待定插值係數。值得注意的是,插值公式 和 都用基本解為基函式,但插值公式 在配點 和源點 重合處,假設了一個源點強度因子(origin intensity factor) 。
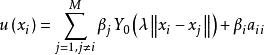 奇異邊界法
奇異邊界法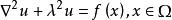 奇異邊界法
奇異邊界法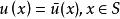 奇異邊界法
奇異邊界法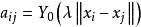 奇異邊界法
奇異邊界法將插值公式 代入方程 和 ,令 ,因為基本解滿足控制方程,我們得到下面矩陣形式的邊界條件離散代數方程:
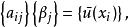 奇異邊界法
奇異邊界法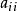 奇異邊界法
奇異邊界法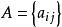 奇異邊界法
奇異邊界法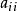 奇異邊界法
奇異邊界法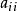 奇異邊界法
奇異邊界法源點強度因子 實際上是插值矩陣 的對角線元素。由於基本解的原點奇異性,我們不能夠簡單地用基本解插值基函式來計算 。理想的方法是從數學理論上導出一個計算源點強度因子的公式,但目前這是一個非常有挑戰性的數學物理問題。下面我們通過反插值技術來求解源點強度因子 。
反插值技術
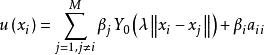 奇異邊界法
奇異邊界法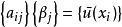 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法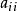 奇異邊界法
奇異邊界法注意到插值公式 和離散代數方程 中的待求插值係數 與邊界上的配點分布,邊界條件和右邊項有關,而源點強度因子 僅依賴於邊界條件和邊界上的配點分布,與右邊項無關。因而,我們可以設計一個反插值技術來計算對角線元素。
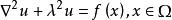 奇異邊界法
奇異邊界法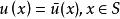 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法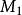 奇異邊界法
奇異邊界法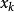 奇異邊界法
奇異邊界法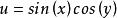 奇異邊界法
奇異邊界法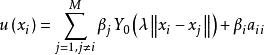 奇異邊界法
奇異邊界法對方程 和 所描述的Helmholtz有限域問題,在其物理域的邊界上布置 個配點 ,在物理域內部布置 個計算輔助點 。對於有基本解的控制方程,容易發現它們的一些已知特解。對Helmholtz方程,有許多已知的簡單特解,例如 。利用插值公式 ,我們有
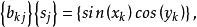 奇異邊界法
奇異邊界法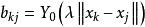 奇異邊界法
奇異邊界法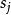 奇異邊界法
奇異邊界法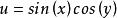 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法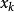 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法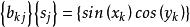 奇異邊界法
奇異邊界法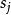 奇異邊界法
奇異邊界法這裡 , 是在邊界配點上的影響係數。因為輔助點和配點完全不重疊,因而沒有奇異性問題。由方程,我們就可以求得影響係數 。
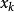 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法這裡內部輔助點的個數可以等於或多於邊界配點的數目。本文中採取兩種方案:
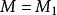 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法方案1——在物理區域內部布置與邊界配點相等數目的輔助點(即),可以得到插值方陣;
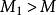 奇異邊界法
奇異邊界法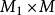 奇異邊界法
奇異邊界法方案2——在物理區域內部布置輔助點的數目多於邊界配點數(即),可以得到插值矩陣,需用移動最小二乘近似求解。
 奇異邊界法
奇異邊界法下一步,我們將計算輔助點換成邊界源點,即配點和源點完全重疊在邊界上;我們有
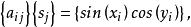 奇異邊界法
奇異邊界法 奇異邊界法
奇異邊界法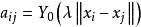 奇異邊界法
奇異邊界法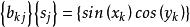 奇異邊界法
奇異邊界法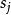 奇異邊界法
奇異邊界法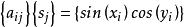 奇異邊界法
奇異邊界法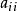 奇異邊界法
奇異邊界法這裡插值矩陣的非對角線元素可由公式得到。因而利用方程中求得的係數,我們就能用方程計算出關鍵的未知對角元素,即源點強度因子。
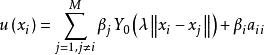 奇異邊界法
奇異邊界法利用上面得到的源點強度因子,我們就可以用邊界插值公式,計算具有相同幾何形狀和控制方程的任意問題。

