太陽系內的引力定律
正文
太陽系內各天體之間引力相互作用所遵循的規律。十七世紀六十年代，牛頓首先研究月球的運動，發現它基本上符合平方反比規律。但是，牛頓不知道如何計算有限體的引力，這就使他的研究拖延下來。就在牛頓進行這些研究的同時，哈雷、雷恩和胡克等好幾位學者也都認識到：如果行星軌道是正圓，那么克卜勒第三定律就包含了平方反比定律。但他們不知道當行星沿橢圓運動時，向心加速度該怎樣計算，於是便向牛頓求教。牛頓證明：在和距離平方成反比的引力作用下，行星的運動將符合經驗的克卜勒定律。接著牛頓又完成了他對月球運動的計算。這樣，經過二十多年的研究，牛頓提出了一個描述宇宙中物體之間相互作用的定量的物理定律。對於當時的觀測技術來說，牛頓萬有引力定律以驚人的精度解釋了太陽系天體的運動。十九世紀中葉,英國J.C.亞當斯和法國勒威耶根據對天王星運動的研究，彼此獨立地以1°的精度預報了海王星的位置。這是牛頓萬有引力定律的一個輝煌成果。但是隨著觀測技術的發展，以牛頓萬有引力定律為基礎的大行星運動理論逐步暴露出一些不足之處，在實際觀測值與理論計算值之間出現了系統的偏差，其中最突出的是水星近日點進動問題。這就不免引起人們對牛頓萬有引力定律的懷疑，由此導致一系列的研究。人們對平方反比定律提出了疑問：引力定律
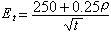中的n是否正好等於2？勃特蘭首先認為n應大於2。A.霍爾支持這種思想， 他根據對水星的研究具體地定出 n=2+1.6×10-7。紐康根據對四顆內行星的研究，得出n=2+1.574×10-7。紐康的這一結論儘管未給出任何物理解釋，但至今仍在許多天文年曆中使用。可是，當人們用這一結論來研究月球的運動時，又出現了矛盾。E.W.布朗根據多年的研究指出：牛頓萬有引力定律完全符合月球的運動情況；如果n大於2的話，那最多也不會超過4×10-8。 十九世紀電磁理論的進展推動了整個物理學的發展，同時這種理論也被套用於研究天體運動。韋伯首先提出，質量為m物體的引力勢應表示為：
。
接著黎曼提出，萬有引力應改為：。
此外，拉普拉斯在早些年代裡也探求過引力傳播速度和宇宙間介質對引力的吸收問題。儘管這些理論都未能被天文觀測證實，都未能全面充分地解釋天體的運動，但它們對引力的物理本質卻進行了許多有意義的探索，並將場與輻射等概念引入引力研究的範疇。1915年愛因斯坦提出著名的廣義相對論，把引力解釋為空間的屬性。廣義相對論更好地解釋了各大行星近日點的進動，但它對太陽系天體運動理論的影響遠遠不止於此。當前，在大行星星曆表的計算中除了考慮萬有引力外，還考慮了廣義相對論的引力非線性迭置效應和行星引起的空間彎曲。
在牛頓萬有引力定律中還有一個令人注意的問題：引力常數G到底是不是常數？如果G在減小，那就意味著引力在減弱（見物理常數的變化）。1937年狄拉克提出：引力常數將與宇宙年齡成反比。此外，還有幾種以馬赫原理為基礎的引力理論，在這些理論中，科學家們都預言 G隨著宇宙年齡的增長而減小。但這些都只是哲學性的探討。弗蘭登根據他近二十年來對月掩星的研究，發現月球有一個難以解釋的加速度。他在排除了太陽風、輻射壓、電磁效應、行星際物質阻尼以及太陽的質量損失等各種因素對月球運動的影響後提出:這是由G的減小而引起的。同時他還解釋了原來地月系潮汐理論中遺留下來的一些疑難。當前對這個問題看法還很不一致，有待進一步的檢驗。
