大型規劃

大型規劃，是指包括大型線性規劃和大型非線性規劃。

大型規劃

正文

包括大型線性規劃和大型非線性規劃。數學規劃得到廣泛套用的主要原因是存在求解大型問題的有效的電腦程式。求解大型問題的關鍵是利用問題的特殊結構。大型線性規劃問題的約束矩陣一般都十分稀疏（即大多數元素是零），且非零元素按一定次序排列，例如，除少數的行和列外，均沿主對角線排列。大型非線性規劃一般也是稀疏結構，且線性項的比例很高，非線性項也有特殊結構，如可分結構等。
大型線性規劃　求解大型線性規劃問題的方法可分為兩類：直接法和分解法。直接法是用一個現存的算法來求解一類特定的問題。大型線性規劃問題多採用直接法求解，基本工具是改進單純形法，主要計算問題是求逆程式。在特殊的矩陣結構下只需要存儲一個約化矩陣。實用電腦程式能有效地求解 8000～16000行的大型線性規劃問題。若模型具有廣義上界結構，可用廣義上界算法GUB求解規模更大的問題。
分解法又稱分塊法，它的主導思想是把原系統分成若干獨立的子系統求解，再用適當的方法來考慮各子系統之間的影響。1970年美國數學家M.D.梅薩羅維茨提出分解－協調算法。這種算法的設計思想來自大系統的多級遞階控制結構。首先把原問題分解成若干相對獨立的子問題，稱為一級子問題，分別求解，然後再用適當的方法定義一個或若干個二級子問題，來協調一級子問題之間的相互影響，以得到原問題的解。60年代中期曾廣泛流行過的丹齊克－沃爾夫分解算法，現在只有少量商業上的套用。其主要原因是這種算法在計算上存在不穩定性和電腦程式的複雜性。
大型非線性規劃　求解大型非線性規劃的方法有兩類：可分規劃和近似規劃。可分規劃的特點是任一非線性函式都是可分的，即

。

因此每個非線性函式可按格點集上的點分段線性化，從而把非線性可分規劃變成線性規劃。可分規劃對於大部分是線性函式並具有凸可分非線性函式的問題是一種有效的算法，其實用電腦程式可求解數千行數千列的大型非線性規劃問題。
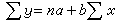近似規劃是利用線性規劃程式作為子程式來處理一般形式的非線性函式。設大型非線性規劃問題是：

式中min表示求極小值,s.t.表示約束條件；xj為線性變數，y為非線性變數的m維向量，gi為非線性函式。所有變數均有上界和下界。給定初始基點向量y0，每個函式gi都近似地是這個點的線性化函式：　

式中Δy =y-y0，而墷gi是gi的梯度向量。用此線性化函式代替每個gi，就把原問題約化為線性規劃問題。規定Δy的上界和下界，即－ε≤Δy≤ε，求解此線性規劃，得到Δy*，把它加到y0上得到新的基點,計算對應的梯度向量墷gi，必要時可減小ε,然後重複上述過程。現在已有近似規劃的通用程式和專用程式。
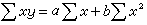
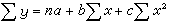
大型網路流問題　利用線性規劃基變數的樹結構，可用單純形法求解有數十萬個節點或弧的網路問題。其解法比最有效的網路算法更快。

配圖

相關連線