理論及計算
定義
基爾霍夫電壓定律表明：
沿著閉合迴路所有元件兩端的電勢差（電壓）的代數和等於零。
或者描述為：
沿著閉合迴路的所有電動勢的代數和等於所有電壓降的代數和。
以方程表達，對於電路的任意閉合迴路有：
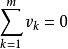基爾霍夫電壓定律其中，m 是這閉合迴路的元件數目，v 是元件兩端的電壓，可以是實數或複數。
基爾霍夫電壓定律不僅套用於閉合迴路，也可以把它推廣套用於迴路的部分電路。
電場與電勢
在靜電學裡，電勢定義為電場的負線積分：
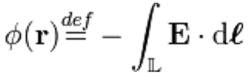基爾霍夫電壓定律其中，Φ(r) 是電勢，E 是電場，L 是從參考位置到位置 r 的路徑，dl 是這路徑的微小線元素。那么，基爾霍夫電壓定律可以等價表達為：
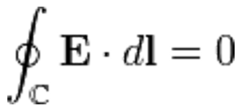基爾霍夫電壓定律其中，C 是積分的閉合迴路。
這方程乃是法拉第電磁感應定律對於一個特殊狀況的簡化版本。假設通過閉合迴路 C 的磁通量為常數，則這方程成立。
這方程指明，電場沿著閉合迴路 C 的線積分為零。將這線積分切割為幾段支路，就可以分別計算每一段支路的電壓。
實際套用方法
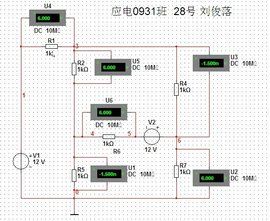
套用該方程時，應先在迴路中選定一個繞行方向作為參考，則電動勢與電流的正負號就可規定如下： 電動勢的方向 (由負極指向正極)與繞行方向一致時取正號，反之取負號; 同樣，電流的方向與繞行方向一致時取正號，反之取負號。例如，用此規定可將迴路(如圖2)的基爾霍夫電壓方程寫成：
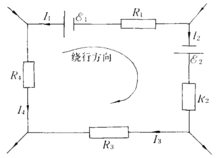圖2 電路中的迴路-E+E=-IR+IR+IR3-IR
每個閉合迴路均可列出一個方程。如果某迴路至少有一個支路未被其他方程用過，則稱此迴路為獨立迴路。對於存在M個獨立迴路的電路，可以列出M個獨立的迴路電壓方程，它們組成的方程組稱為基爾霍夫第二方程組。
適用範圍
基爾霍夫定律建立在電荷守恆定律、歐姆定律及電壓環路定理的基礎之上，在穩恆電流條件下嚴格成立。當基爾霍夫第一、第二方程組聯合使用時，可正確迅速地計算出電路中各支路的電流值。由於似穩電流(低頻交流電) 具有的電磁波長遠大於電路的尺度，所以它在電路中每一瞬間的電流與電壓均能在足夠好的程度上滿足基爾霍夫定律。因此，基爾霍夫定律的套用範圍亦可擴展到交流電路之中。
它除了可以用於直流電路的分析，和用於似穩電路的分析，還可以用於含有電子元件的非線性電路的分析。運用基爾霍夫定律進行電路分析時，僅與電路的連線方式有關，而與構成該電路的元器件具有什麼樣的性質無關。
但用於交流電路的分析是，即對通過含時電流的電路進行分析時，由於通過閉合迴路的磁通量是時間的函式，根據法拉第電磁感應定律，會有電動勢E出現於閉合迴路 C 。所以，電場沿著閉合迴路 C 的線積分不等於零。此時迴路方程應寫作：
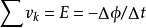基爾霍夫電壓定律(磁場正方向與迴路正方向相同時)
這是因為電流會將能量傳遞給磁場；反之亦然，磁場亦會將能量傳遞給電流。
對於含有電感器的電路，必需將基爾霍夫電壓定律加以修正。由於含時電流的作用，電路的每一個電感器都會產生對應的電動勢E。必需將這電動勢納入基爾霍夫電壓定律，才能求得正確答案。
