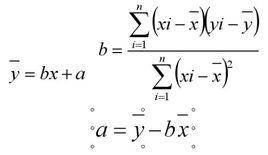定義
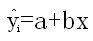①式若：在一組具有相關關係的變數的數據（x與Y）間，通過散點圖我們可觀察出所有數據點都分布在一條直線附近，這樣的直線可以畫出許多條，而我們希望其中的一條最好地反映x與Y之間的關係，即我們要找出一條直線，使這條直線“最貼近”已知的數據點，記此直線方程為（如右所示，記為①式）這裡在y的上方加記號“^”，是為了區分Y的實際值y，表示當x取值Xi=1，2，……，6）時，Y相應的觀察值為Yi，而直線上對應於Yi的縱坐標是 ①式叫做Y對x的 回歸直線方程，相應的直線叫做 回歸直線，b叫做回歸係數。
計算方法
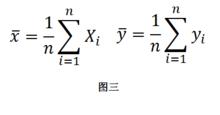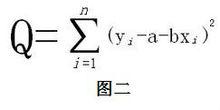回歸直線方程
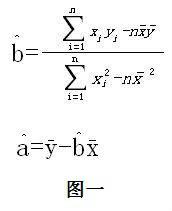回歸直線方程
回歸直線方程
回歸直線方程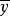
回歸直線方程
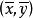回歸直線方程要確定回歸直線方程①，只要確定a與回歸係數b。回歸直線的求法通常是最小二乘法：離差作為表示xi對應的回歸直線縱坐標y與觀察值yi的差，其幾何意義可用點與其在回歸直線豎直方向上的投影間的距離來描述。數學表達:Yi-y^=Yi-a-bXi.總離差不能用n個離差之和來表示，通常是用離差的平方和即(Yi-a-bXi)^2計算。即作為總離差，並使之達到最小，這樣回歸直線就是所有直線中除去最小值的那一條。這種使“離差平方和最小”的方法，叫做最小二乘法。用最小二乘法求回歸直線方程中的a,b有圖一和圖二所示的公式進行參考。其中， 和 如圖三所示，且 稱為樣本點的中心。
