概述
 單周期庫存模型
單周期庫存模型 對於單周期需求來說,庫存控制的關鍵在於確定訂貨批量。訂貨量就等於預測的需求量。
由於預測誤差的存在,根據預測確定的訂貨量和實際需求量不可能一致。如果需求量大於訂貨量,就會失去潛在的銷售機會,導致機會損失——即訂貨的機會(欠儲)成本。另一方面,假如需求量小於訂貨量,所有未銷售出去的物品將可能以低於成本的價格出售,甚至可能報廢還要另外支付一筆處理費。這種由於供過於求導致的費用稱為陳舊(超儲)成本。顯然,最理想的情況是訂貨量恰恰等於需求量c
為了確定最佳訂貨量,需要考慮各種由定貨引起的費用。由於只發出一次訂貨和只發生一次訂購費用,所以訂貨費用為一種沉沒成本,它與決策無關。庫存費用也可視為一種沉沒成本,因為單周期物品的現實需求無法準確預計,而且只通過一次訂貨滿足。所以即使有庫存,其費用的變化也不會很大。因此,只有機會成本和陳舊成本對最佳訂貨員的確定起決定性的作用。確定最佳訂貨量可採用期望損失最小法、期望利潤最大法或邊際分析法。
示例
按過去的記錄,新年期間對某商店掛曆的需求分布率如表1所示:
 單周期庫存模型
單周期庫存模型 已知:每份掛曆的進價為C=50元,售價P=80元。若在1個月內賣不出去,則每份掛曆只能按S=30元賣出。求:該商店應該進多少掛曆為好。
解:設該商店買進Q份掛曆當實際需求d< 時,將有一部分掛曆賣不出去,每份超儲損失為Co="C-S=50-30=20(元);">
•當實際需求d > Q 時,將有機會損失,每份欠儲損失為Cu=P-C=80-50=30(元)。
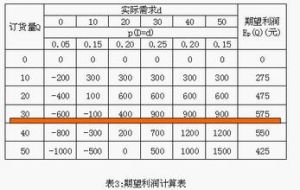
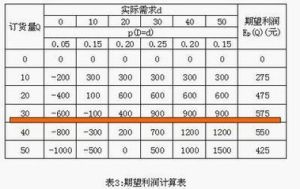
•當Q=30時,則E_l(Q)=[30×(40-30)×0.20+30×(50-30)×0.15]+[20×(30-0)×0.05+20×(30-10)×0.15+20×(30-20)×0.20]=280(元)。
•當Q取其它值時,可按同樣方法算出EL(Q),結果如表2所示,由表2可以得出最佳訂貨量為30份。
邊際分析法
假定原計畫訂貨量為D,考慮追加一個單位訂貨的情況。追加1個單位的訂貨,使得期望損失變化,如果Q為最佳訂貨量,則無論增加或減少都應使損失加大。
則臨界缺貨機率:
含義
當實際需求大於訂貨量D的機率P(D)等於時,D就是最佳的訂貨量。若不存在一個D,使得成立,則滿足條件且最小的D就是。確定了,然後再根據經驗分布就可以找出最佳訂貨量。
某批發商準備訂購一批聖誕樹供聖誕節期間銷售。該批發商對包括訂貨費在內的每棵聖誕樹要支付$2,樹的售價為$6。未售出的樹只能按$1出售。節日期間聖誕樹需求量的機率分布如表4所示(批發商的訂貨量必須是10的倍數)。試求該批發商的最佳訂貨量。
查表可知,實際需求大於50棵的機率為0.25,再結合求D* 的條件可以求出最佳訂貨量為50棵。
Tidy found serious XHTML errors Saved in parser cache with key wikidb:pcache:idhash:85161-0!1!0!!zh!2!zh and timestamp 20090404162016