哈特曼流動
正文
在相互垂直的電磁場作用下，不可壓縮粘性導電流體沿均勻矩形截面管道的定常層流運動。它是一種簡單形式的磁流體動力學流動，是J.F.哈特曼(1865～1936)於1937年首先用理論分析和實驗證實的，因而得名。如圖1所示,B0是外加均勻恆穩磁場；E、v是外加電場和流速；管道的上、下面為絕緣壁；前後兩個側面為電極。當壓強梯度推動流體沿y軸流動時,外接負載電路從流體取得電能。若外接電源，則流體通過磁場力將電源的電能變成自己的機械能。為了突出問題主要方面和簡化計算，假設：①流體不可壓縮並具有粘性和有限電導率；②管道無限長和無限寬，即不考慮電極表面和管道進出口端對流動的影響，而把流動視為只沿管高有變化的一維問題。這種管道流模型的精確解是管高2d比管長L和管寬W小一個數量級以上的管道流的近似解。 如圖2所示，流速、外加磁場和電場分別為 (0，v，0)、(0，0，B0)和（－E，0，0）。作用於任一流體微團Q的徹體力有負的壓強梯度
、粘性力 、 磁場力，其中μ 為動力粘性係數；σ為電導率；By為流體中的電流所產生的y向磁場；v是z的函式，其餘皆為常數。粘性力和流體切割磁力線導致的磁場力是阻礙流動的因素；負壓強梯度和電場導致的磁場力是促使流動的因素。當流體作定常層流流動時，上述四種力平衡，故流動的動力方程為： 
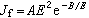(1)
(2)
(3)
式中v0和J0分別為平均流速和平均電流密度；Ha為流體切割磁力線導致的磁場力與粘性力之比的平方根，稱為哈特曼數，即。圖3是根據式(2) 畫出的平均流速不變時不同哈特曼數的速度分布曲線。當Ha=0,即只有粘性力起作用時,速度分布曲線同一般管流的一樣,是拋物線；當Ha》1，即磁場力起主要作用時，速度曲線變平,流速在壁面邊界層內降為零，邊界層厚度約為d/Ha。這是因為在中間平面附近，流體切割磁力線導致的磁場力起主導作用，它阻礙流體流動；而在壁面附近，電場導致的磁場力起主導作用,它加速流體流動，而且這種力愈強,邊界層也愈薄。式(3)說明四種情況：①短路(E=0)時，平均電流最大,平均磁場力也最大，它對流動阻礙最大,這是電磁製動閘的原理；②J0＞0，E厵0時，平均電流和電場反向，外電路從流體取得電能，這是磁流體發電機的原理（見磁流體發電）；③J0=0時，通過測量E,可從式(2)計算流量,這是電磁流量計的原理；④J0＜0時,電流與電場同向,作用在流體上的磁場力加速流體流動,流體從外電路取得電能並通過磁場力轉變為機械能，這是電磁泵或電漿推進器（見電磁推進）的原理。