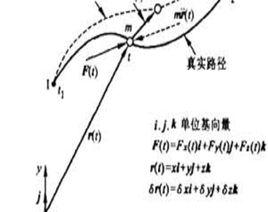
定義
 哈密頓向量場
哈密頓向量場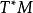 哈密頓向量場
哈密頓向量場假設 ( M,ω) 是一個辛流形。因為辛形式ω 非退化,誘導了切叢與餘切叢 的一個線性同構
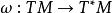 哈密頓向量場
哈密頓向量場以及逆
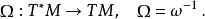 哈密頓向量場
哈密頓向量場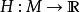 哈密頓向量場
哈密頓向量場從而,流形 M上的1-形式可以與向量場等價起來,故任何可微函式 確定了惟一的向量場 X= Ω(d H),稱為 哈密頓函式 H的 哈密頓向量場。 即對 M上任何向量場 Y,等式
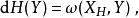 哈密頓向量場
哈密頓向量場一定成立。
注:一些作者定義哈密頓向量場為相反的符號;需注意物理與數學著作的不同習慣。
例子
假設 M是一個 2 n維辛流形。則由達布定理,我們在局部總可以取 M的一個典範坐標
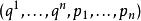 哈密頓向量場
哈密頓向量場在這個坐標系下辛形式表示為
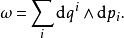 哈密頓向量場
哈密頓向量場則關於哈密頓函式 H的哈密頓向量場具有形式
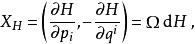 哈密頓向量場
哈密頓向量場這裡 Ω 是一個 2 n× 2 n矩陣
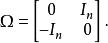 哈密頓向量場
哈密頓向量場性質
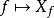 哈密頓向量場
哈密頓向量場映射 線性的,所以兩個哈密頓函式之和變為相應的 哈密頓向量場之和。
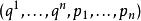 哈密頓向量場
哈密頓向量場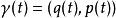 哈密頓向量場
哈密頓向量場假設 是 M上的典範坐標。則曲線 是哈密頓向量場 X的積分曲線若且唯若它是哈密頓方程的一個解:
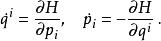 哈密頓向量場
哈密頓向量場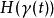 哈密頓向量場
哈密頓向量場哈密頓函式 H在積分曲線上是常數,這就是 與時間 t無關。這個性質對應於哈密頓力學中的能量守恆。
更一般地,如果兩個函式 F與 H的泊松括弧為零(見下),則 F沿著 H的積分曲線為常數;類似地 H沿著 F的積分曲線是常數。這個事實是諾特定理背後的數學原理。
 哈密頓向量場
哈密頓向量場辛形式 在哈密頓流下不變;或等價地,李導數
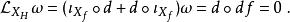 哈密頓向量場
哈密頓向量場 哈密頓向量場
哈密頓向量場這裡 是內乘,用到了李導數的嘉當公式。
泊松括弧
哈密頓向量場的概念導致了辛流形 M上的可微函式的一個斜對稱雙線性運算元,這就是 泊松括弧,由如下公式定義
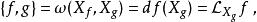 哈密頓向量場
哈密頓向量場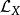 哈密頓向量場
哈密頓向量場這裡 表示沿著向量場 X的李導數。此外,我們可以驗證有恆等式:
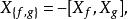 哈密頓向量場
哈密頓向量場這裡右邊表示哈密頓函式 g與 g對應的哈密頓向量場的李括弧。作為一個推論,泊松括弧滿足雅可比恆等式。
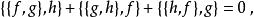 哈密頓向量場
哈密頓向量場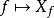 哈密頓向量場
哈密頓向量場這意味著 M上可微函式組成的向量空間,賦予泊松括弧,是 R上的一個李代數,且映射是一個李代數反同態,其核由局部常值函式組成(如果 M連通則為常數)。