原理
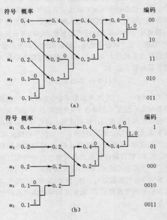圖1 赫夫曼編碼原理設某信源產生有五種符號u1、u2、u3、u4和u5，對應機率P1=0．4，P2=0．1，P3=P4=0．2，P5=0．1。首先，將符號按照機率由大到小排隊，如圖所示。編碼時，從最小機率的兩個符號開始，可選其中一個支 路為0，另一支路為1。這裡，我們選上支路為0，下支路為1。再將已編碼的兩支路的機率合併，並重新排隊。多次重複使用上述方法直至合併機率歸一時為止。從圖（a）和（b）可以看出，兩者雖平均碼長相等，但同一符號可以有不同的碼長，即編碼方法並不唯一，其原因是兩支路機率合併後重新排隊時，可能出現幾個支路機率相等，造成排隊方法不唯一。一般，若將新合併後的支路排到等機率的最上支路，將有利於縮短碼長方差，且編出的碼更接近於等長碼。這裡圖（a）的編碼比（b）好。
赫夫曼碼的碼字（各符號的代碼是異前置碼字，即任一碼字不會是另一碼宇的前面部分，這使各碼字可以連在一起傳送，中間不需另加隔離符號，只要傳送時不出錯，收端仍可分離各個碼字，不致混淆。
實際套用中，除採用定時清洗以消除誤差擴散和採用緩衝存儲以解決速率匹配以外，主要問題是解決小符號集合的統計匹配，例如黑（1）、白（0）傳真信源的統計匹配，採用0和1不同長度遊程組成擴大的符號集合信源。遊程，指相同碼元的長度（如二進碼中連續的一串0或一串1的長度或個數）。按照CCITT標準，需要統計2×1728種遊程（長度），這樣，實現時的存儲量太大。事實上長遊程的機率很小，故CCITT還規定：若l表示遊程長度，則l=64q+r。其中q稱主碼，r為基碼。編碼時，不小於64的遊程長度由主碼和基碼組成。而當l為64的整數倍時，只用主碼的代碼，已不存在基碼的代碼。
長遊程的主碼和基碼均用赫夫曼規則進行編碼，這稱為修正赫夫曼碼，其結果有表可查。該方法已廣泛套用於檔案傳真機中。
定理
在變字長編碼中，如果碼字長度嚴格按照對應符號出現的機率大小逆序排列，則其平 均碼字長度為最小。
現在通過一個實例來說明上述定理的實現過程。設將信源符號按出現的機率大小順序排列為 ：
U： ( a1 a2 a3 a4 a5 a6 a7 )
0.20 0.19 0.18 0.17 0.15 0.10 0.01
給機率最小的兩個符號a6與a7分別指定為“1”與“0”，然後將它們的機率相加再與原來的 a1~a5組合併重新排序成新的原為：
U′： ( a1 a2 a3 a4 a5 a6′ )
0.20 0.19 0.18 0.17 0.15 0.11
對a5與a′6分別指定“1”與“0”後，再作機率相加並重新按機率排序得
U″：（0.26 0.20 0.19 0.18 0.17）…
直到最後得 U″″：（0.61 0.39）
赫夫曼編碼的具體方法：先按出現的機率大小排隊，把兩個最小的機率相加，作為新的機率 和剩餘的機率重新排隊，再把最小的兩個機率相加，再重新排隊，直到最後變成1。每次相 加時都將“0”和“1”賦與相加的兩個機率，讀出時由該符號開始一直走到最後的“1”， 將路線上所遇到的“0”和“1”按最低位到最高位的順序排好，就是該符號的赫夫曼編碼。
例如a7從左至右，由U至U″″，其碼字為0000；
a6按踐線將所遇到的“0”和“1”按最低位到最高位的順序排好，其碼字為0001…
用赫夫曼編碼所得的平均比特率為：Σ碼長×出現機率
上例為：0.2×2+0.19×2+0.18×3+0.17×3+0.15×3+0.1×4+0.01×4=2.72 bit
可以算出本例的信源熵為2.61bit，二者已經是很接近了。
歷史
1951年，
哈夫曼和他在
MIT
資訊理論的同學需要選擇是完成學期報告還是期末
考試。導師Robert M. Fano給他們的學期報告的題目是，尋找最有效的
二進制編碼。由於無法證明哪個已有編碼是最有效的，哈夫曼放棄對已有編碼的研究，轉向新的探索，最終發現了基於有序頻率
二叉樹編碼的想法，並很快證明了這個方法是最有效的。
由於這個算法，學生終於青出於藍，超過了他那曾經和資訊理論創立者
香農共同研究過類似編碼的導師。哈夫曼使用自底向上的方法構建二叉樹，避免了次優算法Shannon-Fano編碼的最大弊端──自頂向下構建樹。
哈夫曼編碼舉例
以
哈夫曼樹─即最優
二叉樹，帶權路徑長度最小的二叉樹，經常套用於
數據壓縮。 在計算機信息處理中，“
哈夫曼編碼”是一種一致性編碼法（又稱“
熵編碼法”），用於數據的無損耗壓縮。這一術語是指使用一張特殊的編碼表將源字元（例如某檔案中的一個符號）進行編碼。這張編碼表的特殊之處在於，它是根據每一個源
字元出現的估算機率而建立起來的（出現機率高的字元使用較短的編碼，反之出現機率低的則使用較長的編碼，這便使編碼之後的字元串的平均期望長度降低，從而達到
無損壓縮數據的目的）。這種方法是由David.A.Huffman發展起來的。 例如，在英文中，e的出現機率很高，而z的出現機率則最低。當利用哈夫曼編碼對一篇英文進行壓縮時，e極有可能用一個位(bit)來表示，而z則可能花去25個位（不是26）。用普通的表示方法時，每個英文字母均占用一個位元組（byte），即8個位。二者相比，e使用了一般編碼的1/8的長度，z則使用了3倍多。倘若我們能實現對於英文中各個字母出現機率的較準確的估算，就可以大幅度提高無損壓縮的比例。
本文描述在網上能夠找到的最簡單，最快速的哈夫曼編碼。本方法不使用任何擴展動態庫，比如STL或者組件。只使用簡單的C
函式，比如：memset，
memmove，qsort，malloc，realloc和memcpy。
因此，大家都會發現，理解甚至修改這個編碼都是很容易的。
背景
哈夫曼壓縮是個無損的壓縮算法，一般用來壓縮文本和
程式檔案。哈夫曼壓縮屬於可變代碼長度算法一族。意思是個體符號（例如，文本檔案中的字元）用一個特定長度的位序列替代。因此，在檔案中出現頻率高的符號，使用短的位序列，而那些很少出現的符號，則用較長的位序列。
編碼使用
我用簡單的C函式寫這個編碼是為了讓它在任何地方使用都會比較方便。你可以將他們放到類中，或者直接使用這個函式。並且我使用了簡單的格式，僅僅輸入輸出
緩衝區，而不象其它文章中那樣，輸入輸出檔案。
bool CompressHuffman(BYTE *pSrc, int nSrcLen, BYTE *&pDes, int &nDesLen);
bool DecompressHuffman(BYTE *pSrc, int nSrcLen, BYTE *&pDes, int &nDesLen);
要點說明
速度
為了讓它(huffman.cpp)快速運行，同時不使用任何動態庫，比如STL或者MFC。它壓縮1M數據少於100ms（P3處理器，主頻1G）。
壓縮
壓縮代碼非常簡單，首先用ASCII值初始化511個
哈夫曼節點：
CHuffmanNode nodes;
for(int nCount = 0; nCount < 256; nCount++)
nodes[nCount].byAscii = nCount;
其次，計算在輸入
緩衝區數據中，每個ASCII碼出現的頻率：
for(nCount = 0; nCount < nSrcLen; nCount++)
nodes[pSrc[nCount]].nFrequency++;
然後，根據頻率進行排序：
qsort(nodes, 256, sizeof(CHuffmanNode), frequencyCompare);
現在，構造
哈夫曼樹，獲取每個ASCII碼對應的位序列：
int nNodeCount = GetHuffmanTree(nodes);
構造哈夫曼樹
構造
哈夫曼樹非常簡單，將所有的節點放到一個佇列中，用一個節點替換兩個頻率最低的節點，新節點的頻率就是這兩個節點的頻率之和。這樣，新節點就是兩個被替換節點的父節點了。如此循環，直到佇列中只剩一個節點（樹根）。
// parent node
pNode = &nodes[nParentNode++];
// pop first child
pNode->pLeft = PopNode(pNodes, nBackNode--, false);
// pop second child
pNode->pRight = PopNode(pNodes, nBackNode--, true);
// adjust parent of the two poped nodes
pNode->pLeft->pParent = pNode->pRight->pParent = pNode;
// adjust parent frequency
pNode->nFrequency = pNode->pLeft->nFrequency + pNode->pRight->nFrequency;
構造哈夫曼樹注意事項
這裡我用了一個好的訣竅來避免使用任何佇列組件。我先前就知道ASCII碼只有256個，但我分配了511個(CHuffmanNode nodes)，前255個記錄ASCII碼，而用後255個記錄
哈夫曼樹中的父節點。並且在構造樹的時候只使用一個
指針數組(ChuffmanNode *pNodes)來指向這些節點。同樣使用兩個
變數來操作佇列索引(int nParentNode = nNodeCount;nBackNode = nNodeCount –1)。
接著，壓縮的最後一步是將每個
ASCII編碼寫入輸出
緩衝區中：
int nDesIndex = 0;
// loop to write codes
for(nCount = 0; nCount < nSrcLen; nCount++)
{
*(DWORD*)(pDesPtr+(nDesIndex>>3)) |=
nodes[pSrc[nCount]].dwCode << (nDesIndex&7);
nDesIndex += nodes[pSrc[nCount]].nCodeLength;
}
(nDesIndex>>3): >>3 以8位為界限右移後到達右邊
位元組的前面
(nDesIndex&7): &7 得到最高位.
注意
在壓縮
緩衝區中，我們必須保存
哈夫曼樹的節點以及位序列，這樣我們才能在
解壓縮時重新構造哈夫曼樹（只需保存ASCII值和對應的位序列）。
解壓縮
解壓縮比構造
哈夫曼樹要簡單的多，將輸入
緩衝區中的每個編碼用對應的ASCII碼逐個替換就可以了。只要記住，這裡的輸入緩衝區是一個包含每個ASCII值的編碼的位流。因此，為了用ASCII值替換編碼，我們必須用位流搜尋哈夫曼樹，直到發現一個葉節點，然後將它的ASCII值添加到輸出緩衝區中：
int nDesIndex = 0;
DWORD nCode;
while(nDesIndex < nDesLen)
{
nCode = (*(DWORD*)(pSrc+(nSrcIndex>>3)))>>(nSrcIndex&7);
pNode = pRoot;
while(pNode->pLeft)
{
pNode = (nCode&1) ? pNode->pRight : pNode->pLeft;
nCode >>= 1;
nSrcIndex++;
}
pDes[nDesIndex++] = pNode->byAscii;
}
程式實例
費諾編碼
#include
#include
#include
#include
#define M 100
typedef struct Fano_Node
{
char ch;
float weight;
}FanoNode[M];
typedef struct node
{
int start;
int end;
struct node *next;
}LinkQueueNode;
typedef struct
{
LinkQueueNode *front;
LinkQueueNode *rear;
}LinkQueue;
//建立佇列
void EnterQueue(LinkQueue *q,int s,int e)
{
LinkQueueNode *NewNode;
//生成新節點
NewNode=(LinkQueueNode*)malloc(sizeof( LinkQueueNode ));
if(NewNode!=NULL)
{
NewNode->start=s;
NewNode->end=e;
NewNode->next=NULL;
q->rear->next=NewNode;
q->rear=NewNode;
}
else
{
printf("Error!");
exit(-1);
}
}
//按權分組
void Divide(FanoNode f,int s,int *m,int e)
{
int i;
float sum,sum1;
sum=0;
for(i=s;i<=e;i++)
sum+=f[i].weight;//
*m=s;
sum1=0;
for(i=s;i
{
sum1+=f[i].weight;
*m=fabs(sum-2*sum1)>fabs(sum-2*sum1-2*f[i+1].weight)?(i+1):*m;
if(*m==i) break;
}
}
void main()
{
int i,j,n,max,m,h[M];
int sta,end;
float w;
char c,fc[M][M];
FanoNode FN;
LinkQueueNode *p;
LinkQueue *Q;
//初始化隊Q
Q=(LinkQueue *)malloc(sizeof(LinkQueue));
Q->front=(LinkQueueNode*)malloc(sizeof(LinkQueueNode));
Q->rear=Q->front;
Q->front->next=NULL;
printf("\t***FanoCoding***\n");
printf("Please input the number of node:");
//輸入信息
scanf("%d",&n);
//超過定義M,退出
if(n>=M)
{
printf(">=%d",M);
exit(-1);
}
i=1; //從第二個元素開始錄入
while(i<=n)
{
printf("%d weight and node:",i);
scanf("%f %c",&FN[i].weight,&FN[i].ch);
for(j=1;j
{
if(FN[i].ch==FN[j].ch)//查找重複
{
printf("Same node!!!\n"); break;
}
}
if(i==j)
i++;
}
//排序(降序)
for(i=1;i<=n;i++)
{
max=i+1;
for(j=max;j<=n;j++)
max=FN[max].weight
if(FN[i].weight
{
w=FN[i].weight;
FN[i].weight=FN[max].weight;
FN[max].weight=w;
c=FN[i].ch;
FN[i].ch=FN[max].ch;
FN[max].ch=c;
}
}
for(i=1;i<=n;i++) //初始化h
h[i]=0;
EnterQueue(Q,1,n); //1和n進隊
while(Q->front->next!=NULL)
{
p=Q->front->next; //出隊
Q->front->next=p->next;
if(p==Q->rear)
Q->rear=Q->front;
sta=p->start;
end=p->end;
free(p);
Divide(FN,sta,&m,end); /*按權分組*/
for(i=sta;i<=m;i++)
{
fc[i][h[i]]="0";
++h[i];
}
if(sta!=m)
EnterQueue(Q,sta,m);
else
fc[sta][h[sta]]="\0";
for(i=m+1;i<=end;i++)
{
fc[i][h[i]]="1";
++h[i];
}
if(m==sta&&(m+1)==end)
//如果分組後首元素的下標與中間元素的相等，
//並且和最後元素的下標相差為1，則編碼碼字字元串結束
{
fc[m][h[m]]="\0";
fc[end][h[end]]="\0";
}
else
EnterQueue(Q,m+1,end);
}
for(i=1;i<=n;i++) /*列印編碼信息*/
{
printf("%c:",FN[i].ch);
printf("%s\n",fc[i]);
}
system("pause");
}
編碼解碼
#include
#include
#include
#define N 100
#define M 2*N-1
typedef char * HuffmanCode[2*M];//haffman編碼
typedef struct
{
int weight;//權值
int parent;//父節節點
int LChild;//左子節點
int RChild;//右子節點
}HTNode,Huffman[M+1];//huffman樹
typedef struct Node
{
int weight; //葉子結點的權值
char c; //葉子結點
int num; //葉子結點的二進制碼的長度
}WNode,WeightNode[N];
/***產生葉子結點的字元和權值***/
void CreateWeight(char ch[],int *s,WeightNode CW,int *p)
{
int i,j,k;
int tag;
*p=0;//葉子節點個數
//統計字元出現個數,放入CW
for(i=0;ch[i]!="\0";i++)
{
tag=1;
for(j=0;j
if(ch[j]==ch[i])
{
tag=0;
break;
}
if(tag)
{
CW[++*p].c=ch[i];
CW[*p].weight=1;
for(k=i+1;ch[k]!="\0";k++)
if(ch[i]==ch[k])
CW[*p].weight++;//權值累加
}
}
*s=i;//字元串長度
}
/********創建HuffmanTree********/
void CreateHuffmanTree(Huffman ht,WeightNode w,int n)
{
int i,j;
int s1,s2;
//初始化哈夫曼樹
for(i=1;i<=n;i++)
{
ht[i].weight =w[i].weight;
ht[i].parent=0;
ht[i].LChild=0;
ht[i].RChild=0;
}
for(i=n+1;i<=2*n-1;i++)
{
ht[i].weight=0;
ht[i].parent=0;
ht[i].LChild=0;
ht[i].RChild=0;
}
for(i=n+1;i<=2*n-1;i++)
{
for(j=1;j<=i-1;j++)
if(!ht[j].parent)
break;
s1=j; //找到第一個雙親為零的結點
for(;j<=i-1;j++)
if(!ht[j].parent)
s1=ht[s1].weight>ht[j].weight?j:s1;
ht[s1].parent=i;
ht[i].LChild=s1;
for(j=1;j<=i-1;j++)
if(!ht[j].parent)
break;
s2=j; //找到第二個雙親為零的結點
for(;j<=i-1;j++)
if(!ht[j].parent)
s2=ht[s2].weight>ht[j].weight?j:s2;
ht[s2].parent=i;
ht[i].RChild=s2;
ht[i].weight=ht[s1].weight+ht[s2].weight;//權值累加
}
}
/***********葉子結點的編碼***********/
void CrtHuffmanNodeCode(Huffman ht,char ch[],HuffmanCode h,WeightNode weight,int m,int n)
{
int i,c,p,start;
char *cd;
cd=(char *)malloc(n*sizeof(char));
cd[n-1]="\0";//末尾置0
for(i=1;i<=n;i++)
{
start=n-1; //cd串每次從末尾開始
c=i;
p=ht[i].parent;//p在n+1至2n-1
while(p) //沿父親方向遍歷,直到為0
{
start--;//依次向前置值
if(ht[p].LChild==c)//與左子相同,置0
cd[start]="0";
else //否則置1
cd[start]="1";
c=p;
p=ht[p].parent;
}
weight[i].num=n-start; //二進制碼的長度(包含末尾0)
h[i]=(char *)malloc((n-start)*sizeof(char));
strcpy(h[i],&cd[start]);//將二進制字元串拷貝到指針數組h中
}
free(cd);//釋放cd記憶體
system("pause");
}
/*********所有字元的編碼*********/
void CrtHuffmanCode(char ch[],HuffmanCode h,HuffmanCode hc,WeightNode weight,int n,int m)
{
int i,k;
for(i=0;i
{
for(k=1;k<=n;k++) /*從weight[k].c中查找與ch[i]相等的下標K*/
if(ch[i]==weight[k].c)
break;
hc[i]=(char *)malloc((weight[k].num)*sizeof(char));
strcpy(hc[i],h[k]); //拷貝二進制編碼
}
}
/*****解碼*****/
void TrsHuffmanTree(Huffman ht,WeightNode w,HuffmanCode hc,int n,int m)
{
int i=0,j,p;
printf("***StringInformation***\n");
while(i
{
p=2*n-1;//從父親節點向下遍歷直到葉子節點
for(j=0;hc[i][j]!="\0";j++)
{
if(hc[i][j]=="0")
p=ht[p].LChild;
else
p=ht[p].RChild;
}
printf("%c",w[p].c); /*列印原信息*/
i++;
}
}
/*****釋放huffman編碼記憶體*****/
void FreeHuffmanCode(HuffmanCode h,HuffmanCode hc,int n,int m)
{
int i;
for(i=1;i<=n;i++)//釋放葉子結點的編碼
free(h[i]);
for(i=0;i
free(hc[i]);
}
void main()
{
int i,n=0; /*n為葉子結點的個數*/
int m=0; /*m為字元串ch[]的長度*/
char ch[N]; /*ch[N]存放輸入的字元串*/
Huffman ht; /*Huffman二叉數*/
HuffmanCode h,hc; /*h存放葉子結點的編碼，hc 存放所有結點的編碼*/
WeightNode weight; /*存放葉子結點的信息*/
printf("\t***HuffmanCoding***\n");
printf("please input information :");
gets(ch); /*輸入字元串*/
CreateWeight(ch,&m,weight,&n); /*產生葉子結點信息，m為字元串ch[]的長度*/
printf("***WeightInformation***\n Node ");
for(i=1;i<=n;i++) /*輸出葉子結點的字元與權值*/
printf("%c ",weight[i].c);
printf("\nWeight ");
for(i=1;i<=n;i++)
printf("%d ",weight[i].weight);
CreateHuffmanTree(ht,weight,n); /*產生Huffman樹*/
printf("\n***HuffamnTreeInformation***\n");
printf("\ti\tweight\tparent\tLChild\tRChild\n");
for(i=1;i<=2*n-1;i++) /*列印Huffman樹的信息*/
printf("\t%d\t%d\t%d\t%d\t%d\n",i,ht[i].weight,ht[i].parent,ht[i].LChild,ht[i].RChild);
CrtHuffmanNodeCode(ht,ch,h,weight,m,n); /*葉子結點的編碼*/
printf(" ***NodeCode***\n"); /*列印葉子結點的編碼*/
for(i=1;i<=n;i++)
{
printf("\t%c:",weight[i].c);
printf("%s\n",h[i]);
}
CrtHuffmanCode(ch,h,hc,weight,n,m); /*所有字元的編碼*/
printf("***StringCode***\n"); /*列印字元串的編碼*/
for(i=0;i
printf("%s",hc[i]);
system("pause");
TrsHuffmanTree(ht,weight,hc,n,m); /*解碼*/
FreeHuffmanCode(h,hc,n,m);
system("pause");
}
Matlab實現
Matlab 中簡易實現Huffman編解碼：
n=input('Please input the total number: ');
hf=zeros(2*n-1,5);
hq=[];
for ki=1:n
hf(ki,1)=ki;
hf(ki,2)=input('Please input the frequency: ');
hq=[hq,hf(ki,2)];
end
for ki=n+1:2*n-1
hf(ki,1)=ki;
mhq1=min(hq);
m=size(hq);
m=m(:,2);
k=1;
while k<=m%del min1
if hq(:,k)==mhq1
hq=[hq(:,1:(k-1)) hq(:,(k+1):m)];
m=m-1;
break
else
k=k+1;
end
end
k=1;
while hf(k,2)~=mhq1|hf(k,5)==1%find min1 location
k=k+1;
end
hf(k,5)=1;
k1=k;
mhq2=min(hq);
k=1;
while k<=m%del min2
if hq(:,k)==mhq2
hq=[hq(:,1:(k-1)) hq(:,(k+1):m)];
m=m-1;
break
else
k=k+1;
end
end
k=1;
while hf(k,2)~=mhq2|hf(k,5)==1%find min2 location
k=k+1;
end
hf(k,5)=1;
k2=k;
hf(ki,2)=mhq1+mhq2;
hf(ki,3)=k1;
hf(ki,4)=k2;
hq=[hq hf(ki,2)];
end
clc
choose=input('Please choose what you want:\n1: Encoding\n2: Decoding\n3:.Exit\n');
while choose==1|choose==2
if choose==1
a=input('Please input the letter you want to Encoding: ');
k=1;
while hf(k,2)~=a
k=k+1;
if k>=n
display('Error! You did not input this number.');
break
end
end
if k>=n
break
end
r=[];
while hf(k,5)==1
kc=n+1;
while hf(kc,3)~=k&hf(kc,4)~=k
kc=kc+1;
end
if hf(kc,3)==k
r=[0 r];
else
r=[1 r];
end
k=kc;
end
r
else
a=input('Please input the metrix you want to Decoding: ');
sa=size(a);
sa=sa(:,2);
k=2*n-1;
while sa~=0
if a(:,1)==0
k=hf(k,3);
else
k=hf(k,4);
end
a=a(:,2:sa);
sa=sa-1;
if k==0
display('Error! The metrix you entered is a wrong one.');
break
end
end
if k==0
break
end
r=hf(k,2);
end
choose=input('Choose what you want:\n1: Encoding\n2: Decoding\n3:.Exit\n');
clc;
end
if choose~=1&choose~=2
clc;
end
