介紹
將交叉熵引入計算語言學消岐領域,採用語句的真實語義作為交叉熵的訓練集的先驗信息,將機器翻譯的語義作為測試集後驗信息。計算兩者的交叉熵,並以交叉熵指導對歧義的辨識和消除。實例表明,該方法簡潔有效.易於計算機自適應實現。交叉熵不失為計算語言學消岐的一種較為有效的工具。
在資訊理論中,交叉熵是表示兩個機率分布p,q,其中p表示真實分布,q表示非真實分布,在相同的一組事件中,其中,用非真實分布q來表示某個事件發生所需要的平均比特數。從這個定義中,我們很難理解交叉熵的定義。下面舉個例子來描述一下:
假設現在有一個樣本集中兩個機率分布p,q,其中p為真實分布,q為非真實分布。假如,按照真實分布p來衡量識別一個樣本所需要的編碼長度的期望為:
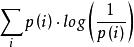 交叉熵
交叉熵H(p)=
但是,如果採用錯誤的分布q來表示來自真實分布p的平均編碼長度,則應該是:
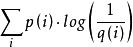 交叉熵
交叉熵H(p,q)=
此時就將H(p,q)稱之為交叉熵。交叉熵的計算方式如下:
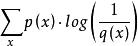 交叉熵
交叉熵對於離散變數採用以下的方式計算:H(p,q)=
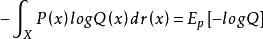 交叉熵
交叉熵對於連續變數採用以下的方式計算:
套用
交叉熵可在神經網路(機器學習)中作為損失函式,p表示真實標記的分布,q則為訓練後的模型的預測標記分布,交叉熵損失函式可以衡量p與q的相似性。交叉熵作為損失函式還有一個好處是使用sigmoid函式在梯度下降時能避免均方誤差損失函式學習速率降低的問題,因為學習速率可以被輸出的誤差所控制。
在特徵工程中,可以用來衡量兩個隨機變數之間的相似度。
在語言模型中(NLP)中,由於真實的分布p是未知的,在語言模型中,模型是通過訓練集得到的,交叉熵就是衡量這個模型在測試集上的正確率。

