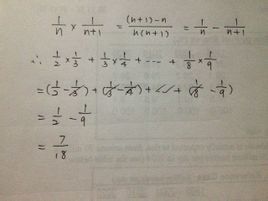簡介
 簡算
簡算方法
1、“4.9+0.1-4.9+0.1”這是國小數學第八冊練習二十七第二題中的一道非常簡單的常見簡便運算題。當給學生布置了這道題後,以為學生會毫不猶豫地使用加法交換率和結合率,順利完成此題,但是當我批改學生的作業時,卻發現了以下三種情況:
(1)、4.9+0.1-4.9+0.1=(4.9-4.9)+(0.1+0.1);
(2)、4.9+0.1-4.9+0.1=4.9-4.9+0.1+0.1;
(3)、4.9+0.1-4.9+0.1=(4.9+0.1)-(4.9+0.1)。
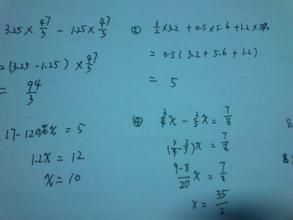 簡算
簡算面對學生的不同觀點,我進行了總結。我首先肯定了學生的學習精神,然後,闡述了觀點:第(1)種解法絕對正確,毫無疑問,但是第(2)種解法也有道理,也不失為一種合理的簡便運算,因為它們都抓住了這道題的關鍵所在,二者沒有本質的區別。簡便運算不能僅僅停留在追求形式上,更應該抓住實質上的簡便,正如那些學生所說4.9-4.9不用算就知道得0,只需要計算0.1+0.1就行了,既然不加括弧同樣也能達到同樣的效果,就沒有必要強調必須加上括弧,簡便運算最終要得就是“簡便”的效果。
2、“88×25”這是一道關於乘法的簡便運算題。當時剛學完乘法分配率,習題中有這樣一道題(80+8)×25,學生完成後,我隨即將該題改為“88×25”讓學生考慮,第二天學生匯報了兩種答案:
(1)、88×25=80×25+8×25=2000+200=2200;
(2)、88×25=11×(8×25)=11×200=2200。
然後,我請學生分別介紹了他們的想法,他們的想法非常好,他們是這樣說的:第(1)種是把88分成80+8,再利用 乘法分配率,讓他們分別同25相乘;第(2)種則將88分成8×11,然後利用乘法交換率和結合率,先把8與25相乘,最後再乘11。
聽完學生的介紹後,我進行了總結,首先肯定了兩種答案的正確,然後對兩種答案進行了分析:兩種答案的共同之處在於都發現了8與25相乘非常簡便,於是想方設法對88進行分解,因此都把握住了這道題的關鍵,所以都是正確的;兩種解法的區別是,分解的方法不同,第(1)種解法是用 加法進行的分解,所以使用的是 乘法分配率,第(2)種解法用乘法進行的分解,所以使用的是乘法交換率和結合率。方法不同卻有異曲同工之處。
最後,再次強調:簡便運算的思路會有很多,但是,只要把握“簡便”這個解題關鍵,正確、合理地使用定律、法則,就應該是正確的。
3、“5436÷18”這是第八冊練習二十七第五題中的一道關於 除法 的簡便運算題。正是因為題目的要求是“下面各題,怎樣簡便就怎樣算”,所以學生的答案可謂是多種多樣,我匯總了一下,主要有以下四種:
(1)、直接算就非常簡便;
(2)、5436÷18=5400÷18+36÷18=300+2=302;
(3)、5436÷18=5436÷9÷2=604÷2=302;
(4)、5436÷18=5436÷6÷3=906÷3=302。
仔細分析,除了第(1)種解法不符合簡便運算規則外,其餘三種解法都有道理,第(2)種解法成功地把 乘法分配率運用到了 除法上;第(3)種和第(4)種解法則將 除數18成功分解成兩個一位因數的積,然後運用“A÷(B×C)=A÷B÷C”這個性質進行連除,把除數是兩位數的除法計算,變成可以口算的除數是一位數的計算,從而使計算簡便。所以,我在課堂上把這四種解法全部公布在黑板上,並引導學生逐一進行了分析,使學生對簡便運算的實質有了進一步地理解。
4、許多學生都頭疼這樣的題“計算下面各題,能簡算的要簡算”,的確這種題確有難度,因為,它不僅要求學生能明確 運算順序,正確計算,而且還要求學生有一定的觀察能力,甚至要有一些直覺,能夠進行合理的分析,找出其中能夠進行簡便運算的部分,併合理地進行簡便運算。要想順利能完成這種題,學生必須對簡算的理解要透,要把握簡算的本質,既不能漏了哪處可以簡算的題,也不能把不能簡算的題錯誤地進行了簡算。
教學過程中我是這樣處理的:首先,我並沒有直接要求學生做這樣的題,而是做了大量的直接簡算的題,列舉了各種不同思路,就像上面那樣,通過練習,引導學生總結出一些常見的簡算數對象“25和4”、“125和8”、“5與任何偶數”以及其他的可以湊整的數,同時使學生對簡算有了比較深刻的理解,甚至有些學生有了對簡便運算的直覺。然後,再重溫了混合運算的 運算順序,使學生對運算順序進一步加深認識,使學生基本上能做到不假思索就能按正常順序完成。最後,再進行此類題。這時,學生已經有了簡算的基礎,對簡算產生了直覺,同時又牢固地掌握了正常情況下的混合運算,就已經不再認為這種題很難了,有些學生甚至認為這種題更好算,不知不覺地把這種方法運用到了其他的地方比如其他計算、 套用題的計算、現實生活等等,從而使學生的計算能力大幅度提高。
通過這些練習,不僅使學生學會了單純的簡便運算,更重要的是,使學生初步理解了學以致用的道理,真正理解了書本上的知識必須運用到實際當中去的道理。
簡便運算是一種高級的混合運算,是混合運算的技巧,學好了簡便運算,不僅能提高計算能力、計算速度,更重要的是,使學到的定義、定理、定律、法則、性質、規律等達到融會貫通的境界,是計算題中最能鍛鍊學生思維能力、開拓學生思路的一種題型,所以,在計算題教學中必須重視簡便運算,注重簡便運算靈活的思路的學習,正確理解簡便運算的涵義,合理地進行簡便運算,使學生的思維能力得到提高。
例題
難度為簡單的:210÷7÷6 1035-(497+235) 210÷(7×6)
1100÷25 2700÷25÷4 246-78+54
難度為中等的:355+260+140+245 98×101 48×125 645-180-245
38×99+38 3500÷14÷5 175×56+25×56 50×25×20×40
較高難度的:1、199999+19999+1999+199+19
2、999×718+333×666
常用乘積
25×2=50
25×3=75
25×4=100
25×8=200
125×3=375
125×4=500
125×8=1000
625×16=10000