含義
向量 AB=a(AB上面有→,a上面有→)的大小(或長度)叫做向量的模,記作|AB|(AB上有→)或| a |(a上面有→)。
計算公式
空間向量(x,y,z),其中x,y,z分別是三軸上的坐標,模長是:
根號下(x^2+y^2+z^2)。
其中x^2表示x的平方。
平面向量(x,y),模長是:
根號下(x^2+y^2)
對於向量x屬於n維復向量空間
x=(x1,x2…,xn)
x的模為‖x‖=sqrt((x,x*))(x與x共軛的內積再開方)
向量性質
向量的模的運算沒有專門的法則,一般都是通過餘弦定理計算兩個向量的和、差的模。
多個向量的合成用正交分解法,如果要求模一般需要先算出合成後的向量。
模是絕對值在二維和三維空間的推廣,可以認為就是向量的長度。推廣到高維空間中稱為范。
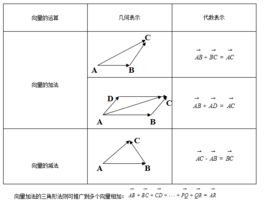
運算法則
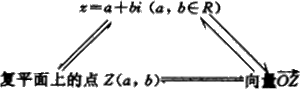 向量的模
向量的模1、模只有大小,是個實數,|a|≥0;
2、|a|^2=a*a=a^2;
3、|a+b|^2=|a|^2+2a*b+|b|^2=a^2+2a*b+b^2;
4、||a|-|b||≤|a±b|≤|a|+|b|;
5、若a=(x,y),則|a|=√(x^2+y^2)