定義
可行集是指資本市場上由風險資產可能形成的所有投資組合的總體。由N種證券所形成的所有組合的集合,它包括了現實生活中所有可能的組合。也就是說,所有可能的組合將位於可行集的邊界上或內部。
將所有可能投資組合的期望收益率和標準差關係描繪在期望收益率-標準差坐標平面上,如下圖 所示。封閉曲線上及其內部區域表示可行集,其邊界上或邊界內的每一點代表一個投資組合。
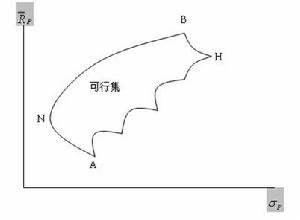 可行集
可行集分析
一般來說,可行集的形狀象傘形,如圖中由A、N、B、H所圍的區域所示。在現實生活中,由於各種證券的特性千差萬別。因此可行集的位置也許比圖中的更左或更左,更高或更低,更胖或更瘦,但它們的基本形狀大多如此。
可行集的左側邊界是一條雙曲線的一部分,而整個可行集呈雨傘狀。按馬科威茨投資組合選擇的前提條件,投資者為理性個體,服從不滿足假定和迴避風險假定,他們在決策時,遵循有效集定理(Efficient Set Theorem):既定風險水平下要求最高收益率;既定預期收益率水平下要求最低風險。
在圖中,滿足第一條原則的組合為從E點到H點再到G點的邊界,之下的點可以全部不用考慮;E為最小風險點,G為最大風險點。
滿足第二條原則的組合為從F點到E點再到H點間的邊界,則弧FEH之右的點可以完全去除,F、H分別為期望收益率的最大點和最小點。而同時滿足兩條原則的,只剩下弧EH邊界,稱為有效集(有效邊界—Efficient Frontier)。理性投資者僅從有效集中進行投資組合選擇。有效邊界的一個重要特性是上凸性。即,隨著風險增加,預期收益率增加的幅度減慢。
在某種意義上,有效邊界是“客觀”確定的,即如果投資者對證券的收益率、方差、協方差有相同的估計,則他們會得到完全相同的有效邊界。
