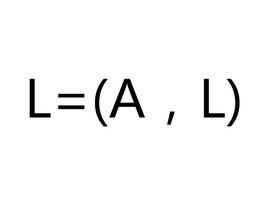基本介紹
語集指二元系統L=(A,L),其中A為由元素a,a,…,a組成的有限集,L為若干詞組成,是一類組合構形。
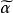 語集
語集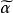 語集
語集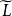 語集
語集 語集
語集所謂詞是以A的若干元素組成的序串,如α=aa…a,L中的詞稱為語集L的可行詞,並約定空集∅為可行詞,對於L的每一可行詞α=aa…a,做集合={a,a,…,a},這樣的構成集族,記為F。於是,語集L=(A,L)導致組合系統=(A,F)。反之,亦可由組合系統構造語集。
例如,擬陣M=(E,I)按如下方式構造語集:A為擬陣M的獨立集,E的元素組成的序串α=a,a,…,a為語集L的可行詞,若且唯若α的字母均不相同,而且對於i=1,2,…,k,對稱差:
A△{a}△{a}△…△{a}
均為M的獨立集。因此,語集這種有序系統亦可視作組合系統 。
語集的性質
語集的性質一般由詞的遺傳性質和詞的替換性質刻畫。換言之,可行詞的哪一部分稱為因子——仍為可行詞,而交換性質通常有如下的三條規定:
 語集
語集 語集
語集1.aa…a為可行詞,對於A的元素a,aa…a卻不是可行詞,則有a存在使得aa……a為可行詞,這裡表示將a從詞中消去。
2.對於可行詞α,β,若α的長度小於β的長度,記為l(α)<l(β),則在β中有子詞β′存在,使得l(β′)≥l(β)-l(α),且αβ為可行詞。
3.對於可行詞α,β,若l(α)<l(β),則在β中有a使得αa為可行詞。
稱詞的元素均不相同的語集為 簡單語集;而詞中相鄰的元素均不相同的語集,稱為 正常語集。
 語集
語集從形式上,可以在語集上引入組合系統的一些基本概念,稱L的極大可行詞為L的基詞,而在上對於任意子集X,定義秩函式
r(X)=max{|I|:I⊆X且I∈F}.
但是,它們能起多大作用,只能視具體情況而定 。