古德斯坦定理

進制表示”的概念定義的。 進制表示，但通常的n 進制表示對古德斯坦定理是不夠的。

簡介

古德斯坦定理是由魯賓·古德斯坦提出的一條關於自然數的命題，即所有古德斯坦序列最終均結束於0。古德斯坦本人用集合論方法證明了這個定理，科比和帕里斯則在1982年證明了該命題在皮亞諾公理系統內是不可證的。

問題陳述

繼承n進制表示

古德斯坦序列是由一種稱為“繼承n進制表示”的概念定義的。這種表示十分類似於通常的n進制表示，但通常的n進制表示對古德斯坦定理是不夠的。
普通的n進制表示（n為大於1的自然數）中，任意的自然數m被寫作n的冪的倍數的和：
m=ak*n^k+a(k-1)*n^(k-1)+...+a0，
其中每個係數ai滿足0≤ai<n，且ak≠0。例如，在二進制下，
35=32+2+1=2^5+2^1+2^0。
所以35的2進制表示就是2^5+2^1+2^0。（可寫作二進制的100011。）同樣地，可將100用3進制表示：
100=81+18+1=3^4+2*3^2+1。
注意指數本身並不寫作n進制。例如，上面的表示就包含2^5和3^4。
要把通常的n進制表示轉換為繼承n進制表示，首先把所有的指數改寫為n進制，然後改寫指數的指數，以此類推，直到每一個在這個表示中出現的數字都不比n大。
例如，35的繼承2進制表示：
35=2^2^2+1+2+1；
100的繼承3進制表示：
100=3^(3+1)+2*3^1+1。

古德斯坦序列

一個自然數m的古德斯坦序列G(m)是一個自然數序列。這個序列的第一個元素就是m本身。要得到第二個元素，首先把m寫作繼承2進制表示，把其中所有的2改為3，然後再減1；這就是G(m)的第二個元素。要得到第三個元素，把第二個元素寫成繼承3進制表示，把所有3改為4，再減1。一直繼續到結果為0，此時這個序列終止。
儘管古德斯坦序列常常增長得快得驚人，古德斯坦定理指出每個古德斯坦序列最終終止於0。

定理證明

古德斯坦定理可以用超出皮亞諾公理系統的手段證明如下：給定一個古德斯坦序列G(m)，我們為之構造一個由序數組成的平行序列，這個平行序列的下界就是G(m)。如果這個平行序列中的項能夠降到0，那么G(m)的項最終也必定降到0。
這個平行序列的構造方法如下：給定G(m)中的第n項的繼承(n+1)進制表示，將其中所有的n+1換成第一個無限序數ω。序數的加法、乘法、乘冪是有標準定義的，所以這樣替換的結果是一個序數，並且這個序數顯然不會比原來的項小。古德斯坦序列中，“更改進制數”的操作不會影響這個序數：把4^4^4+4中的所有4直接換成ω，和先換成5再換成ω是沒有本質區別的。另一方面，在原數上減1，一定會導致使對應的序數減小，例如在5進制的時候，5^5^5+5減1變成5^5^5+4，對應的序數則從ω^ω^ω+ω變成ω^ω^ω+4。由於所有序數在其自然序下構成一個良序集，不存在無窮的單調下降的序數序列，所以這個平行序列一定會終止於0，此時G(m)也為0。定理得證。

變體

科比和帕里斯提出了古德斯坦定理的一個變體：“九頭龍遊戲”。

問題描述

“九頭龍”是一棵有根樹。它的每個樹葉稱為一個頭，與頭相連的邊稱為這個頭的頸。

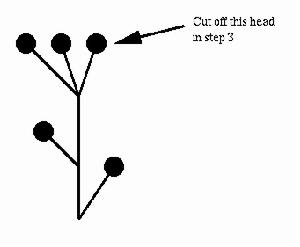砍掉頭之前

九頭龍的初始狀態可以是任意有限的有根樹。在遊戲的每一步中，遊戲者可以砍掉九頭龍的一個頭和相應的一個頸。若砍掉的頸的另一端連線的結點不是樹根，則以這個結點為根的子樹將複製出一定數量的相同的兄弟，通常取這個數量為遊戲的步數，如第3步複製出3個。
因為頭的數目增長得極快，所以這個遊戲的持續時間可能十分漫長。只要在有限步內能夠將九頭龍砍到只剩一個根的狀態，就算遊戲者勝利。
對這個遊戲，有如下定理：
古德斯坦定理變體：無論使用任何策略，遊戲者一定會勝利。

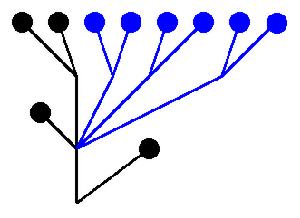砍掉頭之後

證明

定理的證明和原定理類似，是通過對遊戲的每一步構造一個序數實現的。
對任一棵有根樹，按照下面的方法遞歸地定義它對應的序數：
一個頭對應序數0；
一棵有n棵子樹，分別對應序數α1，α2，……，αn的樹，對應的序數為ω^α1+ω^α2+……+ω^αn。
根據此定義，圖中的兩棵樹分別對應ω^（ω^3+1）+1和ω^（ω^2*4+1）+1。由歸納法可證，砍頭操作總是對應序數的減小，但是不存在無窮的單調下降的序數序列，所以遊戲必然以遊戲者的勝利而告終。