序數

集合論基本概念之一，是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的，而良序集又是偏序集、全序集的特殊情形。實數集上的通常的大小關係、集合之間的被包含關係、自然數之間的可整除關係都是偏序的例。顯然，在全序集中xy，三者必居其一且僅居其一。對於全序集〈A，≤〉如果再加上條件⑤A的任一非空子集都有最小元,就稱≤為A上的良序,〈A，≤〉稱為良序集。可寫成α·λ，稱為兩個序數α,λ的乘積。

基本概況

序數是集合論基本概念之一，是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的，而良序集又是偏序集、全序集的特殊情形。

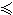序數

偏序、全序和良序次序是二元關係（見映射）的一個非常重要的類型。設R是定義在A上的滿足下列條件的二元關係：①對於一切x∈A有xRx（自反性）；② 對於一切x，y∈A,由xRy與yRx可得x=y（反對稱性）；③對於一切x，y，z∈A，由xRy與yRz可得xRz（傳遞性），就稱R是定義在A上的偏序,也稱半序。偏序R通常記為≤或

，α≤b)讀作α在b前。集合A連同其上定義的偏序≤，稱為偏序集,記為〈A，≤〉。實數集上的通常的大小關係、集合之間的被包含關係、自然數之間的可整除關係都是偏序的例。設≤為A上的偏序。如果在A上定義一個關係<，使得x<滿足條件：①′對任何x∈A，x><稱為嚴格偏序。反之，設><為嚴格偏序,如果定義x≤y若且唯若x>