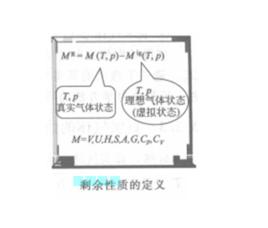
定義
剩餘性質又稱為剩餘函式，其定義為：
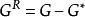剩餘性質上式的物理意義為：剩餘自由焓在相同溫度T和壓力p下真實氣體與理想氣體的自由焓的差值。
通式
表達式
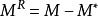剩餘性質上式中，M泛指摩爾熱力學性質，如V、U、H、S或G等。
推導過程
可以用相似的方法定義出其他的性質，如剩餘體積：
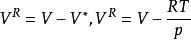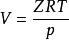剩餘性質
剩餘性質由於，剩餘體積和Z就可以進行關聯，有：
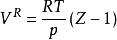剩餘性質按此，就可以寫出剩餘性質的通式：
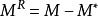剩餘性質上式中，M泛指摩爾熱力學性質，如V、U、H、S或G等。
對於理想氣體
對於理想氣體，有：
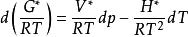剩餘性質又因為
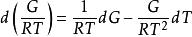剩餘性質兩式相減，得：
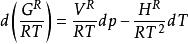剩餘性質上式可套用於恆定組成的流體，是各剩餘性質之間的基本關係式。
注意事項
關於剩餘性質的定義
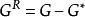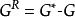剩餘性質
剩餘性質不同書籍對剩餘性質的定義稍有不同，如在Smith、Van ness 和Abbott的書中用的是，而在Kyle的書中用的是，它們的形式基本是一致的，但是相差了一個負號，因此在計算中，一旦選用了一種形式後，就不應再有修改。
本質
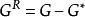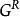剩餘性質
剩餘性質是個假想的性質變化或不可能發生的變化。對於一個物質而言，在相同的溫度和壓力下，真實氣體和理想氣體同時存在往往沒有可能，因此這是個假想的性質變化。但將式用於計算過程中卻是合理的，只要保持計算過程的連貫性。我們知道，可以通討任何途徑來計算不同狀傑下的熱力學件質變化。
與偏離性質的異同
偏離性質，也稱偏離函式，指的是研究態和某一參考點的熱力學函式的差值，對純流體的泛指熱力學性質的偏離函式定義如下：
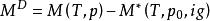剩餘性質此外，有：
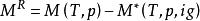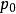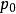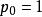剩餘性質
剩餘性質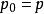 剩餘性質
剩餘性質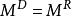
剩餘性質
剩餘性質上述兩個式子除等號右邊的壓力項外，其餘均相同。指的是理想氣體的壓力，雖然的取值沒有限制，但習慣上有兩種方式，一是取單位壓力，其單位與p相同，二是取所研究狀態時的壓力，即。因此，採用第二種取法時，則（以T、p為獨立變數時）。其餘情況下，兩種函式雖然都是熱力學性質的差值，但數值卻有所不同，而其功能卻是類似的。
