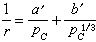簡介
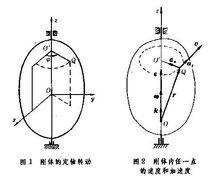
剛體內任一點 Q和其圓周軌跡中心 O'的連線 O' Q（圖1）稱為該點的轉動半徑。從固定平面 Ozx到轉動平面OzQ的轉角 φ，可用來確定該剛體的瞬時位置。轉角 φ隨時間 t的變化規律稱為剛體的轉動方程，寫作：
φ =f（ t）
轉角 φ的變化Δ φ與對應時間間隔Δ t的比值Δ φ/Δ t=ω*稱為平均角速度。當Δ t→0時， ω*所趨的極限 ω稱為（瞬時）角速度，即
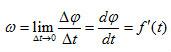剛體定軸轉動當角速度 ω隨時間 t變化時，其變化Δ ω與對應時間間隔Δ t的比值Δ ω/Δ t=ε*稱為平均角加速度。當Δ t→0時， ε*所趨的極限 ε稱為（瞬時）角加速度，即
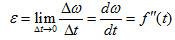剛體定軸轉動剛體的角速度和角加速度都可表示為沿轉軸 Oz（單位矢為 k）的滑動矢量。（圖2）。角速度矢 ω和角加速度矢 ε可分別寫作 ω= ωk， ε= εk。
轉動剛體內任一點 Q的線速度 v等於 v= ω× r，且 v= ω· O´Q。點 Q的線加速度 α為：
α= α+ α= ε× r+ ω× v，
且 α = ε· O´Q ， α= ω· O´Q。
剛體定軸轉動上式中 r為轉軸上任一點 O到點 Q的矢徑，而 α和 α分別是點 Q的切向和法向加速度（見加速度）。
剛體轉動慣量的大小與下列因素有關：
（1）形狀大小分別相同的剛體質量大的轉動慣量大；
（2）總質量相同的剛體，質量分布離軸越遠轉動慣量越大；
（3）對同一剛體而言，轉軸不同，質量對軸的分布就不同，轉動慣量的大小就不同。
