數學定義
利薩茹曲線由以下參數方程定義:
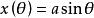 利薩如圖形
利薩如圖形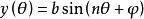 利薩如圖形
利薩如圖形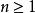 利薩如圖形
利薩如圖形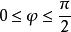 利薩如圖形
利薩如圖形其中,且,
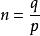 利薩如圖形
利薩如圖形n稱為曲線的參數,是兩個正弦振動的頻率比。若比例為有理數,則,參數方程可以寫作:
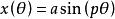 利薩如圖形
利薩如圖形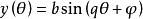 利薩如圖形
利薩如圖形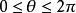 利薩如圖形
利薩如圖形性質
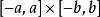 利薩如圖形
利薩如圖形1.若n為無理數,曲線在長方形中稠密。
2.若n為有理數,
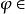 利薩如圖形
利薩如圖形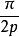 利薩如圖形
利薩如圖形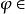 利薩如圖形
利薩如圖形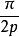 利薩如圖形
利薩如圖形曲線是2q次代數曲線若(0,]對奇數p,或[0,)對偶數p。
 利薩如圖形
利薩如圖形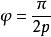 利薩如圖形
利薩如圖形曲線是q次代數曲線的一部份若對奇數p,或對偶數p。
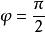 利薩如圖形
利薩如圖形 利薩如圖形
利薩如圖形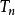 利薩如圖形
利薩如圖形3.若n為偶數而,或若n為奇數而,則曲線是第n個切比雪夫多項式的曲線的一部分。
特別情況
1.若a=b,n=1,則曲線是橢圓。
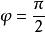 利薩如圖形
利薩如圖形若,則這橢圓其實是圓。
 利薩如圖形
利薩如圖形若,則這橢圓其實是線段。
2.若a=b,n=q=2(所以p=1),則曲線是besace。
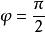 利薩如圖形
利薩如圖形若,則這besace是拋物線一部份。
 利薩如圖形
利薩如圖形若,則這besace是一個熱羅諾雙紐線。
技術套用
藉由使用 利薩茹圖形可以測量出兩個信號的頻率比與相位差。在電工、無線電技術中,常利用示波器來觀察利薩如圖形,並用以測定頻率或相位差。

