提出
該定律由英國劍橋大學教授約翰·伊登斯爾·利特爾伍德提出,發表在他1986年出版的作品集《一個數學家的雜集》里。他提出這個定律的目的是破除人們對超自然現象的迷思。這個定律和巨數定律相關。巨數定律認為,只要樣本數量足夠大,不管多么難以想像的事情都會發生。需要指出這兩個定律都不是經過嚴格證明的統計學定律。
定律內容
利特爾伍德定義“奇蹟”為以百萬分之一機率發生的稀有事件。他假設當一個人在清醒的時候每秒能覺察到一個事件,該事件可能是一個稀有事件,也可能是很平常的事件。利特爾伍德還假設一個人每天有8小時足夠清醒和警覺。因此,在35天時間裡這個人察覺到的事件數就會到達一百萬。於是根據“奇蹟”的定義,平均35天就會有一個所謂的“奇蹟”出現。從這個角度看,我們以為的奇蹟實際並非那么罕見。
利特爾伍德
約翰·伊登斯爾·利特爾伍德(英語: John Edensor Littlewood,1885年6月9日-1977年9月6日),英國數學家,最為出名的是他和高德菲·哈羅德·哈代長期的合作。利特爾伍德出生在肯特郡的羅徹斯特。他在倫敦的聖保羅學校上學,並在那裡受到了F·S·麥考利的教育,現在因為他對理想理論的貢獻而出名。利特爾伍德在劍橋大學三一學院學習,並在1905年的數學Tripos考試中成為Senior Wrangler。在1908年他被選為三一學院的研究員,除了在曼徹斯特大學擔任理察講師的三年外,在他的職業生涯中,他都在劍橋大學度過。1928年,李特爾伍德獲得勞斯‧鮑爾數學教授席位,直到1950年。
他的大部分工作都是在數學分析領域中。他在Ernest William Barnes的指導下開始研究,Barnes說利特爾伍德曾經嘗試過證明黎曼猜想:利特爾伍德證明了如果黎曼猜想是正確的,那么素數定理成立,並可得到誤差項。這項工作使他成為了三一學院的一位研究員。
哈代-勒特伍德圓法
在數學裡, 哈代-勒特伍德圓法是在解析數論中最常被使用的技術之一。其是以高德菲·哈羅德·哈代和約翰·恩瑟·李特爾伍德來命名的,他們是在一連討論華林問題的論文中發展了此一技術。這個觀念一開始的起源通常被歸功於哈代在1916年和1917年中和拉馬努金在整數分拆的漸進分析中之研究。這被許多其他的研究者們所使用,包括哈羅德·達芬波特和維諾格拉多夫,他們稍微地修改了其公式(由複分析移至指數和),但沒有改變大略的內容。上千篇論文使用著此一方法,且直到2005年,這個方法仍然被使用來產生新的成果。
問題中的圓一開始是在複數平面上的單位圓。假定問題一開始是一連串的複數
a,n= 0, 1, 2, 3, ...
想要求得其中的一些可能的漸進類型
a~F(n)
其中有一些啟發性的方法可以用來猜測 F可能的類型,先寫下
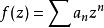 利特爾伍德定律
利特爾伍德定律一個冪級數生成函式。其中有些有趣的例子在於 f的收斂半徑等於1的條件下,故將問題假裝已調整至承現出滿足此一條件。經由此規劃之後,便可以直接由留數定理得出對每個整數 n≥ 0,
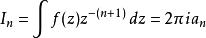 利特爾伍德定律
利特爾伍德定律其中這個積分是繞著圓心為0且半徑為0 < r< 1之 r的圓來積的。
亦即,這是一個閉軌積分,其軌道是一個以逆時鐘方向繞了一圈的圓。為了使其較易回答,可以直接將 r的值取1,即使用單位圓閉軌。但在復變分析中卻有著一些問題,因為 f在單位圓上不一定總是會有定義。圓法在其問題上的做法是強迫將 r值取1,以對 f在單位圓上之奇點的性質有足夠的了解之方式。對其基本的了解可以使用有理數的法里數列,或是等價地使用單位根
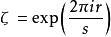 利特爾伍德定律
利特爾伍德定律這裡的分母 s是在 r/s為最簡分數下之分母,可以決定在ζ附近之 f主要奇點的行為之相對的重要性。
哈代-勒特伍德圓法因此可以用複分析的方式來表現出來。當 r趨近 1時的 I的值的分布可以被分成兩個部分,傳統上稱之為 大弧和 小弧。可以將ζ分成兩部分,分別是 s≤ N和 s> N兩部分,其中的 N是一個依方便選定之 n的函式。積分 I可以將其積分範圍分成長度為 s的長度(一樣是依方便選定的),和ζ相連的弧。這些弧可以形成整個圓圈,而其在“大弧”上積分的總和會是2π iF( n)(實際上,會存在一個可掌控的剩餘項)。剩下在“小弧”上的積分總和則可以被一個上界所取代,而且這個上界會數量級地小於 F( n)。
參見
•巧合
•確認偏誤
•巨數定律
•懷疑論
