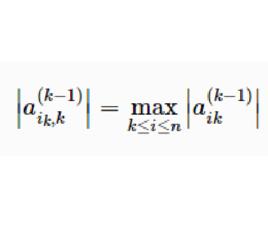針對問題
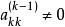 列主元消去法
列主元消去法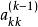 列主元消去法
列主元消去法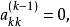 列主元消去法
列主元消去法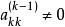 列主元消去法
列主元消去法高斯消去法從第k步到第k+1步的消元過程,必須滿足條件
。而這個元素即被稱為第k步的主元(素)。顯然,高斯消去法是按方程排列的自然順序產生主元的,這樣,一旦出現計算就歸於失敗,而且即使,但若其絕對值很小,也將會因用它作除數,引起其他元素的數量級及舍人誤差急劇增大,導致最終計算結果不可靠。為了避免在高斯消去法套用中可能出現的這類問題,就發展形成了列主元、全主元等多種消去法。這些方法的基本點在於對高斯消去法的過程作某些技術性修改,全面或局部地選取絕對值最大的元素為主元素,從而構成了相應的主元(素)消去法。列主元(素)消去法以處理簡單、相對計算量小的特點,在各類主元消去法中得到最為廣泛的套用。
基本思想
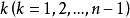 列主元消去法
列主元消去法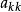 列主元消去法
列主元消去法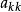 列主元消去法
列主元消去法列主元消去法的基本思想是:在進行第 步消元時,從第k列的 及其以下的各元素中選取絕對值最大的元素,然後通過行變換將它交換到主元素 的位置上,再進行消元。
過程概述
高斯消去法中第k-1步消元得到的結果可由分塊矩陣記為
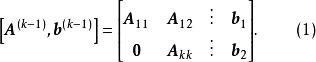 列主元消去法
列主元消去法式中, b、 b為對應於右端常數列的兩個子塊,而
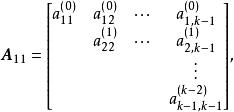 列主元消去法
列主元消去法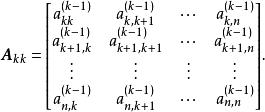 列主元消去法
列主元消去法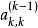 列主元消去法
列主元消去法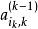 列主元消去法
列主元消去法與高斯消去法不同的是,列主元消去法在第k步消元之前,先在它的第k列主對角元 及其下方的所有元素中(亦即A的第一列元素中)選出絕對值最大的元素 作為這一列的主元,即
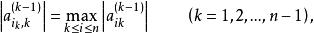 列主元消去法
列主元消去法對式(1),作初等行變換
 列主元消去法
列主元消去法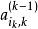 列主元消去法
列主元消去法這樣,就把 換到主對角元位置上。經過選列主元與行交換之後,再如高斯消去法一樣作行的消元變換。上述過程從第一步消元開始執行,即k=1,2,…,n一1,這就構成了 列 主元消去法。綜上可見,列主元消去法僅需矩陣行的交換,因此不發生未知數排列次序的調換。而全主元消去法則要花費相當多的時間選取主元,且還需記錄係數矩陣列交換信息。
算法
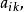 列主元消去法
列主元消去法本算法將消元結果覆蓋 A,乘數m衝掉 方程組解 x存放在 b內。
1) 對於k=1,2,…,n-1,依次做到第5)步;
2) 按列選主元,即確定i,使
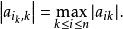 列主元消去法
列主元消去法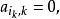 列主元消去法
列主元消去法3) 如果 則輸出無解信息,停機;
4) 如果i=k,則轉向5),否則換行
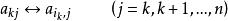 列主元消去法
列主元消去法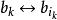 列主元消去法
列主元消去法5) 消元過程
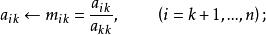 列主元消去法
列主元消去法 列主元消去法
列主元消去法 列主元消去法
列主元消去法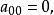 列主元消去法
列主元消去法6) 如果 則停機;
7) 回代求解
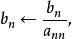 列主元消去法
列主元消去法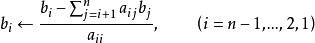 列主元消去法
列主元消去法8) 輸出結果 x。
功能
將矩陣A化為上三角矩陣,然後回代求解線性方程組Ax=b。
MATLAB程式
function z= Gausselimpiv (A,b, ep)
[m,n]=size(A);
if m~=n
disp(’輸入錯誤,係數矩證陣只能是方陣')
end
if n~=length (b)
disp('輸入錯誤,常數項的個數應與方程的個數相同')
end
if nargin==2
ep= eps ;
end
for k=1:n-1
p=A(k,k);I=k;
for i=k:n
if abs (A (i, k)) > abs (p)
end
end
if p<=ep
z=0;
end
if I~=k
for j= k:n
w=A(k,j);A(k,j)=A(I,j);A(I,j)=w;
end
u=b(k);b(k)=b(I);b(I)=u;
end
for i= k+1:n
 列主元消去法
列主元消去法 列主元消去法
列主元消去法 列主元消去法
列主元消去法A(i,k)=A(i,k)/A(k,k);
b(i)=b(i)-A(i,k)
forj=k+1:n
A(i,j)=A(i,j)-A(i,k)A(k,j);
end
end
end
b(n)=b(n)/A(n,n);
fori=(n-1):-1:1
w=0;
forj=(i+1}:n
w=w+A(i,j)b(j);
end
b(i)=(b(i)-w)/A(i,i);
end
z=b;