簡介
理想氣體混合物的分壓定律與分體積定律：
人們在生產和生活實踐中遇到的大多數氣體都是氣體混合物。早在19世紀，科學家在對低壓混合氣體的實驗研究中，就總結出兩條重要的定律，即道爾頓(Dalton)提出的分壓定律和阿馬格(Amagat)提出的分體積定律。
阿馬格分體積定律：
在一個氣體混合物中，任意組分氣體B的分體積定義為
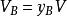分體積定律式中，y是混合氣體中氣體B的摩爾分數，V是混合氣體的總體積。對於一個由N種氣體構成的氣體混合物，必有
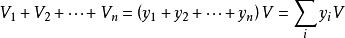分體積定律定律解釋
定律表明，在氣體混合物中，所有組分氣體的分體積之和等於混合氣體的總體積。所以可把分體積V看作組分氣體B對總體積的貢獻。
設溫度為T、壓力為p的容器中，裝有理想氣體混合物，混合氣體的總體積為V，物質的量為n，則
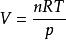分體積定律將此式代入，得
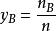分體積定律所以
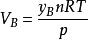分體積定律
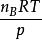分體積定律上式右端 的物理意義是，物質的量為n的理想氣體B在溫度為T、壓力為p時所具有的體積。
於是上式告訴我們：在理想氣體混合物中，某組分氣體的體積等於在相同溫度T和相同壓力p時該氣體單獨存在時所占有的體積。結合式
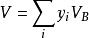分體積定律亦可得出如下結論：混合氣體的總體積等於混合氣體中各組分氣體在與混合氣體具有相同溫度和相同壓力條件下單獨存在時所占有的體積之和。這就是阿馬格分體積定律。分體積定律同樣只適用於理想氣體混合物，對於真實氣體，其各組分的體積不等於它單獨存在時所占有的體積，當然分體積定律不能成立。在低壓下的真實氣體混合物近似服從阿馬格分體積定律。
氣體物質的量分數與分體積的關係
氣體混合物中組分B的分體積與總體積之比可用理想氣體狀態方程得出
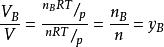分體積定律即
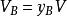分體積定律式中 y——組分B的物質的量分數
此式表明，混合氣體中任一組分的分體積等於該組分的物質的量分數與總體積的乘積。
