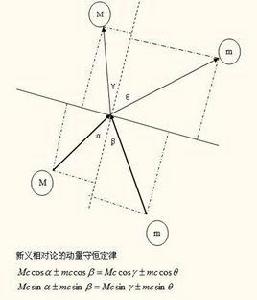
定律簡介
在資訊理論中, 熵被用來衡量一個隨機變數出現的期望值。它代表了在被接收之前,信號傳輸過程中損失的信息量,又被稱為 信息熵。信息熵也稱 信源熵、 平均自信息量。在1948年,克勞德·艾爾伍德·香農將熱力學的熵,引入到資訊理論,因此它又被稱為 香農熵。
熵在生態學中是表示生物多樣性的指標。
詳細內容
最高定律
在等勢面上,熵增原理反映了非熱能與熱能之間的轉換具有方向性,即非熱能轉變為熱能效率可以100%,而熱能轉變成非熱能時效率則小於100%(轉換效率與溫差成正比),這種規律制約著自然界能源的演變方向,對人類生產、生活影響巨大;在重力場中,熱流方向由體系的勢焓(勢能+焓)差決定,即熱量自動地從高勢焓區傳導至低勢焓區,當出現高勢焓區低溫和低勢焓區高溫時,熱量自動地從低溫區傳導至高溫區,且不需付出其它代價,即絕對熵減過程。顯然熵所描述的能量轉化規律比能量守恆定律更重要,通俗地講:熵定律是"老闆",決定著企業的發展方向,而能量守恆定律是"出納",負責收支平衡,所以說熵定律是自然界的最高定律。
分熵的特點
熵概念源於卡諾熱機循環效率的研究,是以熱溫商的形式而問世的,當計算某體系發生狀態變化所引起的熵變總離不開兩點,一是可逆過程;二是熱量的得失,故總熵概念擺脫不了熱溫商這個原始外衣。當用狀態數來認識熵的本質時,我們通過研究發現,理想氣體體系的總微觀狀態數受巨觀的體積、溫度參數的控制,進而得到體系的總熵等於體積熵與溫度熵之和(見有關文章),用分熵概念考察體系的熵變化,不必設計什麼可逆路徑,概念直觀、計算方便(已被部分專家認可),因而有利於教和學。
熵流
熵流是普里戈津在研究熱力學開放系統時首次提出的概念(普里戈津是比利時科學家,因對熱力學理論有所發展,獲得1977年諾貝爾化學獎),普氏的熵流概念是指系統與外界交換的物質流及能量流。我們認為這個定義不太精闢,這應從熵的本質來認識它,不錯物質流一定是熵的載體,而能量流則不一定,能量可分熱能和非熱能[如電能、機械能、光能(不是熱輻射)],當某絕熱系統與外界交換非熱能(發生可逆變化)時,如通電導線(超導材料)經過絕熱系統內,對體系內熵沒有影響,準確地說能量流中只有熱能流(含熱輻射)能引人熵流(對非絕熱系統)。對於實際情形,非熱能作用於系統發生的多是不可逆過程,會有熱效應產生,這時系統出現熵增加,這只能叫(有原因的)熵產生,而不能叫熵流的流入,因能量流不等於熵流,所以不論什麼形式的非熱能流都不能叫熵流,更不能籠統地把能量流稱為熵流。
現實例子
冰櫃不能減熵
克勞修斯把熵增原理表述為:"熱量不能自動地從低溫物體傳向高溫物體”,這給人們一個錯覺,外界做功使熱量從低溫物體傳到高溫物體,或者說使等溫體變成不等溫體,就意味著發生熵減。這種認識是偏面的,以絕熱房間內放一工作的電冰櫃為例,冰櫃內溫度變低,冰櫃外的房間內溫度變高,許多人把這外界做功而拉開溫差的現象叫做熵減。這種看法是錯誤的,僅就室內的冰櫃內外來說,如果考慮了電流的熱效應,這個室內的總熵變化只增不減(不信可計算一下)。外界做功不能使絕熱系統內的熵減少,不論是電能、機械能等非熱能做功(通常不能避免熱效應)都不能使絕熱系統內的熵減少,所以說,我們認為熵增原理準確的表述應為:“在等勢面上,絕熱系統內的熵永不減少”。
地熱來源
地下熱能儲量巨大,相當於全球煤炭儲量的1.7億倍。有人估算,以當今全世界耗能總量計算,即使全部使用地熱能,4100萬年後才能使地球內部的溫度下降 1℃。地熱的特點呈內高外低分布,我們認為(另有論文)它遵循"可壓縮流體的靜力學方程",即勢焓(勢能+焓)平衡規律,當地內勢焓低於地表勢焓時,重力具有雲集地表低溫熱能向地心轉移的機制,地熱是永恆存在的能源。關於地熱來源問題,人們尚無準確定論,主要有兩種解釋:
1.地球內部的放射性元素蛻變放熱,即原子能;
2.地球在形成初期帶來的熱量。我們對上述解釋的看法是,如果是第一種,有三種情況:
①地熱溫度呈外低內高按一定梯度的分布,那熱源必在地心,這不就是核子彈嗎?後果不堪構想;
②礦物分布通常遵循"物以類聚"的原則,那么地球內部的放射性元素分布(熱源)就會與地熱分布一致,顯然這不合情理;
③地下溫泉或岩漿(石頭)應該裹挾著很強的放射性物質,實際上沒有,所以說地熱的主要來源不可能是放射性元素蛻變。如果是第二種,一是體積收縮擠壓產生;二是本來是高溫體,冷卻至今形成熱量梯度分布,這種可能性是有的。我們認為也有第三種可能,即地球形成時溫度是均勻的而又不是十分高溫的物質,從45億年前至今,重力將地表低溫區熱能向地心轉移,使熱量形成梯度分布(中心約5000℃),逐步實現勢焓平衡。
計算公式
1.克勞修斯首次從巨觀角度提出熵概念,其計算公式為:S=Q/T,(計算熵差時,式中應為△Q)
2.波爾茲曼又從微觀角度提出熵概念,公式為:S=klnΩ,Ω是微觀狀態數,通常又把S當作描述混亂成度的量。
3.筆者針對Ω不易理解、使用不便的現狀,研究認為Ω與理想氣體體系的巨觀參量成正比,即:Ω(T)=(T/εT)3/2,Ω(V)=V/εV,得到理想氣體的體積熵為SV=klnΩv=klnV,溫度熵為ST=klnΩT=(3/2)klnT ,計算任意過程的熵差公式為△S=(3/2)kln(T'/T)+kln(V'/V),這微觀與巨觀關係式及分熵公式,具有易於理解、使用方便的特點,有利於教和學,可稱為第三代熵公式。
上述三代熵公式,使用的物理量從形式上看具有"直觀→抽象→直觀"的特點,我們認為這不是概念遊戲,是對熵概念認識的一次飛躍。
引力“熵增減”
一種解釋
引力的“熵減”現象說法——熱環論
科學家們通過長期對熵理論的研究,提出了“熱環論”(又可稱“熱動論”),完成了恩格斯的遺願。
熱環論指出:可壓縮流體的靜力學方程,即勢焓(勢能+焓)平衡規律指出,在引力場中,相同質量的流質其擁有的勢焓值均為同一常數,這就意味著當流質勢能大時其焓值小(溫度低),相反,當勢能小時其焓值大(溫度高),如果星體中心的勢焓值比外圍低時,引力將迫使外圍低溫區熱量向中心高溫區傳導轉移,以趨於勢焓平衡。又根據熱輻射定律可知,熱輻射僅由溫度決定,不受引力影響。上述兩類因素是熱循環的動力,即熱量在引力的幫助下從低溫3k傳導至高溫億萬k(太空中或星體內部都存在著溫度梯度這個客觀事實),再以輻射的方式逸散到太空中去,就這樣循環往復以至無窮,這就"熱環論"描述的現象。
以白矮星為例,白矮星內部無熱源發光是因為星體引力能從太空雲集低溫熱能。任何星體與太空間都存在著相反的熱循環轉移過程,即使是具有內部熱源的星體也 疊加著上述熱循環過程(比如恆星的聚變熱源)。
另一種解釋
引力還是“熵增”現象——熱寂說
這就是著名的“熱寂說”...可以看出來,引力同樣可以解釋為“熵增”現象:質量的引力把原來的物質從低溫加熱到高溫,這個加熱的能量來自物質本身也就是質量的消耗(有可能來自原子核的質量減少,也可能來自電子能級的消耗等因素,下面有分析)。但宇宙的質量一開始怎么來的?至今還在假設當中,這也就是宇宙的誕生之謎。不過能推斷出的就是:宇宙這些“天生”的質量其實就是“負熵”,宇宙一直都是在“負熵”變“正熵”的過程,即質量消耗而變為熱能的過程,所以宇宙如果還有質量,就不會是我們所說的“死亡終結”,有質量就可以創造熱能,從而獲得非熱能形式的能量。所以質量的引力把原來的物質從低溫加熱到高溫,並不是違反熱力學第二定律的:“自發性把熱從低溫物體轉移到高溫物體”,而是消耗了自身獲得熱能,由熵增而變高溫的(這也就是我們所使用的所有能量的本源)。而把熱能還原為質量,而不引起其他影響的,才是“絕對熵減”。
原子與原子之間的分隔是因為有電磁力(電磁力是虛光子傳遞產生的),遠離原子核的電子能級高。以地球為例,地球內部物質被高度擠壓,所以經過壓縮,電子“被迫”降低能級,這就會釋放出能量(電子向低能級躍遷,虛光子轉變為光子釋放出來),釋放的能量又被周圍的物質吸收,導致周圍物質的電子能級升高,運動更劇烈,但運動空間被引力限制,所以形成一個“惡性循環”,也可以看成是一個平衡(用來抵禦壓縮,減緩體積縮小速度):釋放能量,然後吸收,再釋放...逐漸向外圍的低溫區域傳遞,代價就是體積會不斷縮小緊密,最終達到一個“度”,產生新的質變。不過如果不是恆星這樣因為引力巨大,已經快速的經過了一次量變與質變的轉化的(由巨大引力實現的內部更高溫,造成聚變,也就是觸發了更深層的能量釋放...),其他溫和的小天體,比如地球,經歷的這個過程是非常漫長的,這也就導致了來自外界的變數干擾會成為必然,所以僅僅只能理論上成立。
宇宙末日猜測
熱環論,是有一種美好的因素為前提才提出來的,但提出後同樣發現,規律就是規律,不會以意志為轉移...也許真的存在這個“好”的結果,不過也同樣存在兩種“壞”的結局:熱環論與熱寂說正相反,可以推導出的是宇宙的“冷寂”或“大坍塌”...比如星體一樣會不斷壓縮變小,周圍也就會不斷的增加低溫區,低溫區的熱轉移不會或不足以使高溫區的質量和體積增加(可以說是杯水車薪),反而會加劇高溫區的消耗,加快熱輻射的損耗(“惡性循環”,這么看,還是逃不脫“熵增”的“魔咒”:一切都在向無序方向進行,整體的無序里必然會有局部的有序現象...)。如果整個宇宙的質量不足以疊加出足夠強的引力,星體會越來越孤立而變為一片“冷寂”景象,如果質量足夠,最後的結果就是整個宇宙體積會因為引力而收縮——大坍塌,在這個過程中,整個宇宙就可以看成是一個更大的天體,宇宙也會進入“熱寂”的混沌過程,可以說就是“奇點”的形成過程,然後不斷量變導致質變(超高度的壓縮,達到一個“度”,觸發更深層的能量釋放,導致爆炸,然後釋放出新的“基本粒子”...),這就是“奇點爆炸”。如此循環(其實這樣也不算“壞”了)...
是不是有點熟悉?不錯,這也是上面提到的恆星的量變與質變的轉化。那么這“新的基本粒子”同樣是一個很有意思的話題,何為“基本粒子”?呵呵...