方法概述
通過分離參數，用函式觀點討論主變數的變化情況，由此我們可以確定參數的變化範圍.這種方法可以避免分類討論的麻煩，從而使問題得以順利解決.分離參數法在解決有關不等式恆成立、不等式有解、函式有零點、函式單調性中參數的取值範圍問題時經常用到.解題的關鍵是分離出參數之後將原問題轉化為求函式的最值或值域問題.
注意：不要與"分離常數法"混為一談！
套用舉例
例1. 設函式 f(x)=ax^2－3x+1 對於 x ∈ [－1 ， 1] 總有 f(x)≥0 成立，求 a 的取值範圍．
解：對於 x∈[－1，1]，
a x^2－3x+1≥ 0.
故 ax^2≥ 3x－1.
當 x= 0時顯然成立；
若 x不為0，則有 a≥ ( 3x－1) / x^2 = 3/ x－1/ x^2 =9/4－ (1/ x－3/2)^2
設t =1/ x，則 t∈(－ ∞,－1]∪[1, + ∞)；
再設g(t) =9/4 － (t －3/2)^2．
g(t)的圖象是一開口向下的拋物線，在t = 3/2取最大值．
故g(t)≤g(3/2) = 9/4．
也就是說對於 x∈[－1，1]且 x≠0，(3 x－1) / x^2≤9/4.
∴ a≥9/4. 例2．討論關於 x的方程：lg( x－1)+lg(4－ x)=lg( a－ x)的實數解的個數 .
解： 原方程可化為：
( x－1)(4－ x)= a－ x (1< x<4)
a=－ x^2+6 x－4=－( x－3)^ 2+5 (1< x<4)
因為 f( x)=－( x－3) ^2+5的單調區間為：(1，3]，(3，4）
當 x∈(1，3]時， f( x)∈(1，5]；
當 x∈(3，4)時， f( x)∈(4，5)；
所以：當 a∈(4，5)時，方程有兩解；
當 a∈(1，4)或5時，方程有一解；
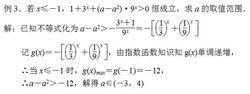分離參數法例3當 a∈(－∞，1]∪(5，+∞)時，原方程無解. 例4． 已知函式 f( x)是定義在[ －1,1]上的奇函式， f(1)=1, 若對 a, b∈[ －1,1] ,且 a+ b≠0,
恆有( f(a)+f(b))/(a+b)>0
(1) 判斷 f( x)在區間[ －1，1]上的單調性.
(2) 若 f( x)≤ a－2 am+1對 x∈[－1，1]， a∈[1，3]恆成立，求 m的取值範圍．
解：（1）易知 f( x)在區間[ －1，1]上為增函式．
（2）由（1）知， f( x)在[－1，1]上單調遞增，且 f(1)=1，則 f( x)在[－1，1]上最大值為1．
∵ f( x)≤ a－2 am+1對 x∈[－1，1]， a∈[1，3]恆成立，
則只需 a^2－2 am+1≥1，即 a^2－2 am≥0對 a∈[1，3]恆成立，
即2 m≤ a對 a∈[1，3]恆成立，∴2 m≤1, m≤1/2
綜上所述， m的取值範圍為（－∞， 1/2].
