定義
波前是指波的等相位面達到的空間。分波前干涉法就是選擇空間不同兩點的光波作為干涉源,實現干涉。根據惠更斯原理,空間任何一個閉合面都可以作為次級波源,遠處的光波是次級波源發出的光波的干涉疊加。分波前正是相當於在這樣的閉合曲面上取至少兩個不同區域讓光透過,以實現干涉。
典型例子
最典型的分波前干涉法,有楊氏雙縫隙干涉、雙孔干涉、光柵干涉。
限制和套用
分波前法是否出現干涉條紋,受光源的空間相干性限制。點光源具有最好的空間相干性,在全空間相干,因此,分波前時可以取距離任意遠的區域的波前都能得到干涉條紋。擴展光源空間相干性不高,分波前時,取的不同區域只有局限在空間相干性良好的範圍內才能得到干涉條紋。根據這一定,分波前法又可以測量光場的空間相干性,從而推測出光源的大小。用空間相干性判斷光源大小的最好例子是麥可遜星體干涉儀。
分波前法干涉
楊氏干涉
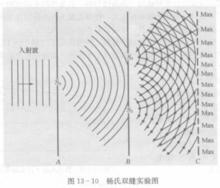 圖1
圖11801年,英國人托馬斯·楊用一個普通光源實現了光的干涉,由於其構思之巧妙,裝置之簡單,條紋之明顯,使得這個實驗在波動光學中具有十分重要的意義,它成為光的波動學說的立論基礎之一,被譽為物理學中最美的實驗之一。
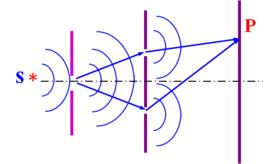
楊認為,雖然每個發光的分子或原子發出的光時斷時續,各個光波的初相位各不相同,但是從同一個光波分開的兩束光應有恆定的相位關係,這就是分波前法干涉。因此,他使一個點光源發出的光通過兩個小孔,將其分成兩個部分,讓它們重新相遇而疊加,結果在屏上觀察到了干涉條紋。楊氏干涉的實驗簡圖如圖1所示。
 圖2
圖2在圖1中,平面單色入射光通過小孔S0,造成一個點光源,由光源S0發出的光波的波前同時到達小孔S1和S2,通過S1和S2後的兩束光在屏C上相遇時出現了如圖2(a)所示的干涉現象。由於S1和S2位於S0發出的光波的同一個波前,S1和S2就可以視為兩個新的相干的子光源,它們發出的兩束光滿足相干條件,因而出現了干涉現象。這種從同一個波前上獲得相干光的方法稱為分波前法。
後來,楊氏用三條狹縫代替上述的三個小孔,每個狹縫相當於一個線光源,其可以認為是由多個點光源沿一條線排列而成。由於每個點光源經雙縫後均產生干涉圖樣,而這些點光源與雙縫的相對位置完全相同,它們產生的干涉圖樣也完全相同。這些相同的圖樣相互疊加起來就使亮點變成亮線,如圖2(b)所示,從而使干涉詳細更為清晰。
洛埃鏡實驗
受楊氏實驗的啟發,人們又先後提出了菲涅耳雙稜鏡實驗、菲涅耳雙平面鏡實驗和洛埃鏡實驗等多種實驗方案,這些實驗都屬於分波前法干涉,它們無一例外地顯示出了光的干涉現象。其中洛埃鏡實驗最值得引起注意,因為它還顯示了光波動性的另一種現象——半波損失現象。
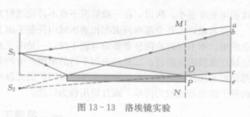 圖3
圖3洛埃(H.Lloyd,1800-1881)在1834年提出的實驗方案更加簡單,他用一塊平板玻璃作反射鏡,用一個狹縫狀光源作為干涉用光源。從狹縫光源發出的光波一部分掠射(即入射角接近90°)到平板玻璃上,經表面反射到達屏上,另一部分直接射到屏上,這兩部分光在屏上相遇疊加,出現了干涉條紋,如圖3所示。
在這個實驗中,反射光可看做是由虛光源S2發出的,S1與S2這一對鏡像光源構成了一對相干光源。有趣的是,若把螢幕移到鏡面邊緣處(即MN的位置),在螢幕與反射鏡的交點O處出現了暗條紋。這一點令人始料不及,因為按照前述干涉的一般理論,由S1與S2發出的兩個光波到達O點相遇時光程差為零,O點應出現明條紋。出現暗條紋的實驗事實說明了由S1發出的光經鏡面反射時一定多走或少走了λ/2的光程,使得直射光和反射光在O點疊加時滿足暗條紋的條件。這種光在鏡面反射時相位發生突變的現象稱半波損失現象(half-wave loss)。
光的半波損失現象得到了其他實驗的進一步證明。現在已經確認,當光在光疏媒質和光密媒質界面反射時,反射光的光程要產生λ/2的突變。光的半波損失現象可以由光的電磁理論給出合理的解釋,因而它成為光的波動說的又一個實驗證據。