歷史
分形幾何的概念是美籍法國數學家曼德布羅特（B.B.Mandelbrot）1975年首先提出的，但最早的工作可追溯到1875年，德國數學家維爾斯特拉斯（K.Weierestrass）構造了處處連續但處處不可微的函式，集合論創始人康托（G.Cantor，德國數學家）構造了有許多奇異性質的三分康托集。 1890年，義大利數學家皮亞諾（G.Peano）構造了填充空間的曲線。1904年，瑞典數學家科赫（H.von Koch）設計出類似雪花和島嶼邊緣的一類曲線。1915年，波蘭數學家謝爾賓斯基（W.Sierpinski）設計了象地毯和海綿一樣的幾何圖形。這些都是為解決分析與拓撲學中的問題而提出的反例，但它們正是分形幾何思想的源泉。
1910年，德國數學家豪斯道夫（F.Hausdorff）開始了奇異集合性質與量的研究，提出分數維概念。1928年布利乾（G.Bouligand）將閔可夫斯基容度套用於非整數維，由此能將螺線作很好的分類。1932年龐特里亞金（L.S.Pontryagin）等引入盒維數。1934年，貝塞考維奇（A.S.Besicovitch）更深刻地提示了豪斯道夫測度的性質和奇異集的分數維，他在豪斯道夫測度及其幾何的研究領域中作出了主要貢獻，從而產生了豪斯道夫-貝塞考維奇維數概念。以後，這一領域的研究工作沒有引起更多人的注意，先驅們的工作只是作為分析與拓撲學教科書中的反例而流傳開來。
原理簡介
fractal dimension主要描述分形最主要的參量，簡稱分維。 通常歐幾里德幾何中，直線或曲線是1維的，平面或球面是2維的，具有長、寬、高的形體是 3 維的；然而對於分形如海岸線、科赫曲線、謝爾賓斯基海綿等的複雜性無法用維數等於 1、2、3 這樣的數值來描述。科赫曲線第一次變換將1英尺的每邊換成3個各長4英寸的線段，總長度變為 3×4×4/3=16 英寸；每一次變換使總長度變為乘以4/3，如此無限延續下去，曲線本身將是無限長的。這是一條連續的回線，永遠不會自我相交，回線所圍的面積是有限的，它小於一個外接圓的面積。因此科赫曲線以它無限長度擠在有限的面積之內，確實是占有空間的 ，它比1維要多，但不及2維圖形，也就是說它的維數在1和2之間，維數是分數。同樣，謝爾賓斯基海綿內部全是大大小小的空洞，表面積是無限大，而占有的 3 維空間是有限的，其維數在2和3之間。
詳細內容
計算分形維數的公式如下
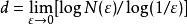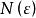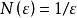分形維數
分形維數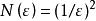
分形維數 分形維數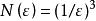
分形維數
分形維數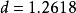
分形維數
分形維數式中 是小立方體一邊的長度， 是用此小立方體覆蓋被測形體所得的數目，維數公式意味著通過用邊長為 的小立方體覆蓋被測形體來確定形體的維數。對於通常的規則物體 ，覆蓋一根單位 長度的線 段所需 的數目要 ，覆蓋一個單位邊長的正方形， ，覆蓋單位邊 長的立方體， 。從這三個式子可見維數公式也適用於通常的維數含義。利用維數公式可算得科赫曲線的維數 ，謝爾賓斯基海綿的維數d=(ln3/ln2)=1.585。對於無規分形，可用不同的近似方法予以計算，也可用一定的適當方法予以測定。
