多重分形

多重分形(multifractal)一種分為多個區域的複雜分形結構。為了對分形的複雜性和不均勻性進行更細緻地刻畫，需引進它的機率分布函式及其各階矩的計算，由此構成了分形維數的一個連續譜，稱之為多重分形或多標度分形。

由於多重分形至今尚無嚴格的數學定義，以下僅通過實例進行簡單的描述.設有一個分布不均勻的分形，首先將它分成若干個小區域，定義第i區域內的密度分布函式為屍，假定屍，存在著標度關係，即

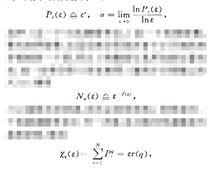多重分形

其中e是一個小的測量單位，a是一個標度指數，稱為奇異指數，它是反映分形體內各個小區間的奇異程度的一個量，所以a的數值與其所在的位置有關.進一步將分形上具有相同a值的小區間數記為

f (a)被稱為奇異譜，因為它將奇異值a的密度用一個連續函式來表示.另一方面，還可將分布函式進行加權求和，得到

r(y)常稱為質量指數.再定義加權後的廣義分形維數D。為

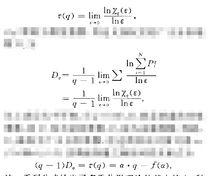多重分形

從上述公式中可知，當9=。時，D。就是普通的分形維數，而D,稱為信息維數，D:稱為關聯維數.因此，幾，被稱為廣義分形維數.經過簡單的計算可得a, 六a)和:<q) }D、這兩組參量之間的對應關係式為

這一系列公式給出了多重分形理論的基本核心.利用多重分形，可把一個複雜的分形分成許多具有不同奇異程度的小區域來研究，從而能分層次地來 了解分形的內部精細結構.